应用型文章
1 | 模版 |
Explainable data-driven formulation of chloride migration coefficient of eco-friendly concrete based on advanced automatic programming
1、研究目标:
给出一个可以解释的数据驱动方法,该方法可以使用人工蜂群表达式编程和基因表达式编程来构建混凝土的氯离子迁移系数公式,目的是克服黑盒机器学习模型的局限同时实现高准确性。
2、难点:
-
传统数据驱动方法对从业者不方便以及缺乏可解释性。
-
在混凝土设计中氯离子迁移性的评估是重要且困难的任务。做实验评估氯离子迁移需要的成本高、时间投入多以及资源需求。
-
需要高效且有效的评估方法。
-
Q:当前的评估方法的参数量有限同时对专门的数据集做各种假设,因此这些方法的泛化性和精度会进行折衷。
- 设计一个可靠、简单的基于物理的模型预测氯离子迁移性同时考虑所有影响因素很困难。
- 许多变量很难用数学表达出来。
A:基于先进表达编程技术,尤其专注于克服可理解性和精度的权衡问题(同时提升透明性和精度),开发高效方法预测氯离子在混凝土中的转移系数。
-
Q:机器学习模型预测混凝土氯离子转移一般都是黑盒模型,即无法给出实际使用的模型公式。
A: 建立实际表达公式可以表示在混凝土中影响氯离子传输的成分之间的复杂化学反应。
-
Q:即使有机器学习模型给出了其模型表示的公式,但是这个公式也是局限在特定混凝土上,因为忽略了关键变量。
A: 调查参数对所提方法的性能的作用以及混合物设计变量对氯离子迁移系数的作用,以对混凝土耐久性提供启发。
3、背景:
混凝土,氯化物,碳排放,
使用数据驱动技术整合混凝土领域的知识包括特征筛选、异常检测和超参选择。
氯离子在钢筋混凝土中的迁移会造成去钝化,加速了腐蚀和混凝土开裂。
补充粘合材料(煤粉、炉渣)在空隙结构中产生细化以及通过化学作用改变氯离子的结合能力。
水灰比直接影响混凝土的孔隙率和空隙联通性,空隙是氯离子传输的主要路径。
自动回归比传统机器学习有优势:
- 提供显示的数学表达式,优于黑盒的机器学习模型。
- 自动回归比传统回归有优势,可以发现变量间的非线性关系和相互作用无需假定数学结构,而传统回归需要假定函数形式。
- 自动回归克服可解释性与精度的权衡问题,实现共同提升。
4、方法:
数据驱动搭建公式的框架:
- 从之前的发布的文章中搜集数据。
- 去除缺失的数据。
- 使用随机森林识别重要的特征变量。
- 使用孤立森里检测异常数据。
- 使用多重共线性分析阻止多重共线性。
- 使用自回归分析对混凝土的Dnssm(non-steady-state migration coefficient)建模。
- 使用性能指标评估从Dnssm得到的结果。
- 展示最优的Dnssm公式。
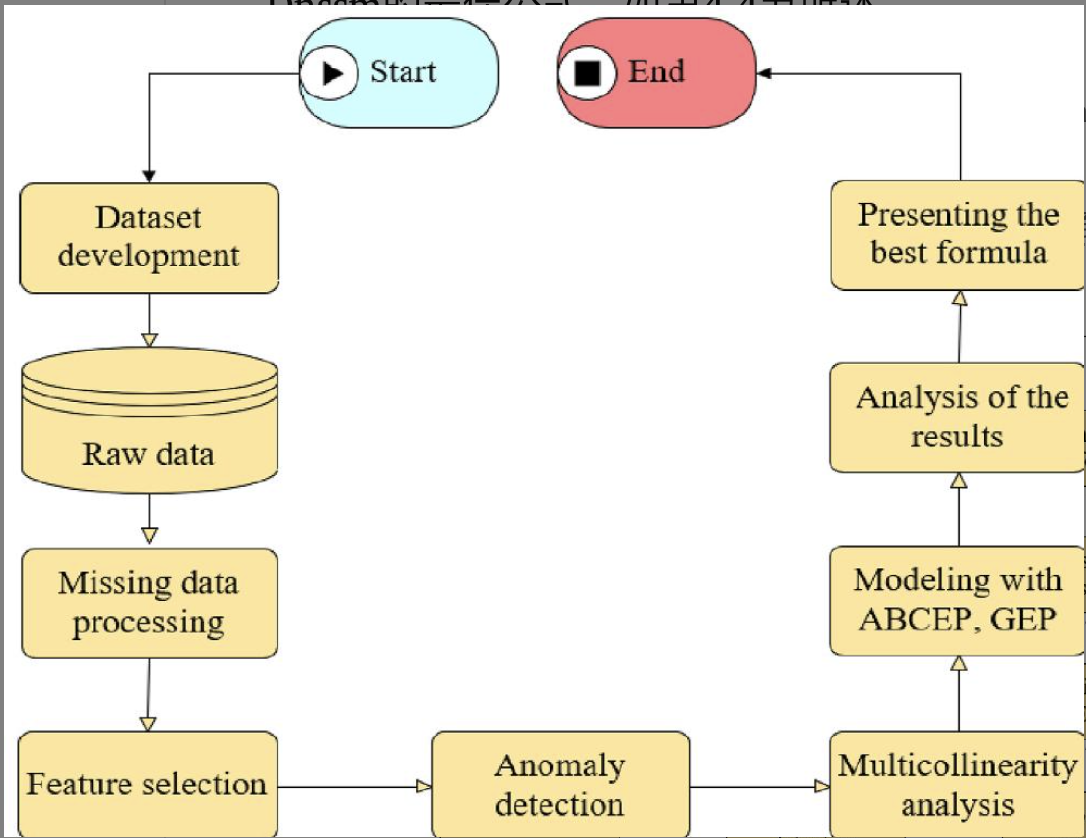
自动回归automatic regression
采用两个自动回归算法,一个是Artificial Bee Colony Expression Programming (ABCEP),另一个是Gene Expression Programming (GEP)
- ABCEP使用群智能原则。
- GEP是具有遗传启发算子的演化算法。
- 两个方法的缺点是在优化时的计算强度和偶然性的公式复杂度的局限性
**Gene Expression Programming **
基因表达编程被开发出来就是为了获取公式。该算法由固定长度的线性染色体以及表达式树构成。
基因型(线性字符串)和表型(非线性表达树)之间可以相互明确翻译属于Karva语言。
基因组或染色体由固定长度的线性符号字符串组成,该字符串由一个或多个等长的基因组成。(二叉树层序输出)
基因结构分为头部和尾部:
- 头部 (Head): 包含函数(如加、减、乘、除、平方根等)和终端(变量或常数)符号。
- 尾部 (Tail): 仅包含终端符号。
- 根据公式$t=h(n-1)+1$ (基因尾部的长度 t; 基因头部的长度h),确保了在头部包含函数和终端符号,尾部只包含终端符号的结构下,所有生成的表达树(ETs)都能是语法正确的,并能完整地从基因中表达出来。
- GEP基因头部的长度(即头部包含的符号数量),这是一个根据具体问题预先选择的参数。
- n:函数集中具有最多参数的函数的参数数量。例如,如果函数集为 {Q,∗,/,−,+},其中 Q(平方根)是单参数,∗,/,−,+是双参数,那么 n=2。
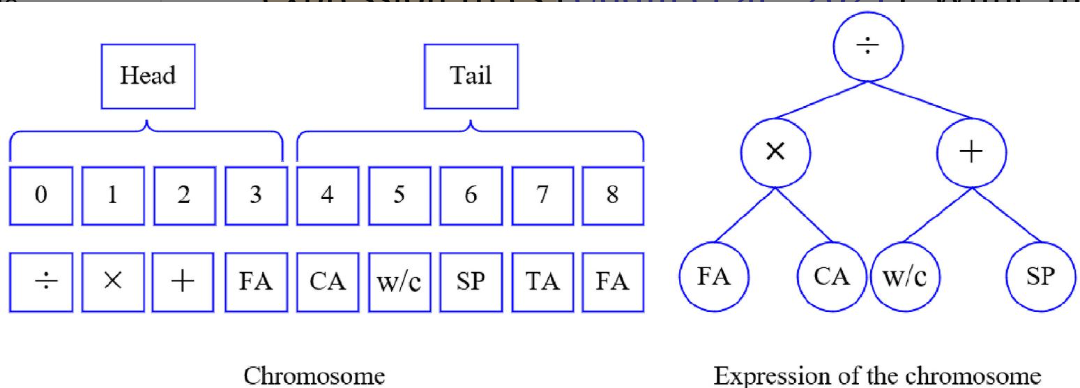
染色体由基因和表达式树构成,表达式树有多种呈现方式,由GEP算法选择最优呈现方式。
表达树是由功能和终端符号组成的树状结构。树的根节点对应基因型的第一个符号,其分支则根据函数的参数数量向下延伸,直到形成一个只包含终端符号的基线。
开放阅读框(ORF)指的是基因中实际编码并能被翻译成表达树(Expression Tree, ET)的部分。
- 终止点与基因末端重合:这表示整个基因序列都被视为有效编码区域,所有的遗传信息都参与到表达树的构建中。在这种情况下,ORF 的长度与基因的固定长度相等。
- 终止点位于基因末端之前(上游):这意味着基因的一部分序列(即 ORF 终止点之后的部分)不参与当前表达树的构建,形成了非编码区域(non-coding regions)。尽管基因的总长度是固定的,但 ORF 的实际有效长度可以小于基因的总长度。
- GEP通过引入非编码区域,将基因型与表现型解耦。基因组是固定的线性符号串,而其中只有开放阅读框(Open Reading Frame, ORF)部分被翻译成表现型(表达树)。非编码区域位于ORF之外,对这些区域的修改不会影响当前表现型的语法正确性,但为未来的进化提供了丰富的变异储备。这使得GEP能够在不牺牲语法正确性的前提下,自由地探索更广阔的搜索空间,从而显著提升了其解决问题的性能和效率,体现了其在进化计算中的“可进化性本质”。
- 尽管每个基因的长度是固定的,但它仍有可能编码不同大小和形状的表达树。
- 最简单的是仅由一个节点组成。
- 最大的是由与基因长度一样多的节点组成(当头部的所有元素都是具有最大元数的函数时)。
- 我们唯一需要注意的是,不要破坏基因的结构组织,始终保持头部和尾部之间的边界,并且不允许在尾部出现代表功能的符号。
基因(准确说是开放阅读框)可独立编码成一个子表达树。每个开放阅读框编码一个结构和功能上独特的子表达式树。根据手头的问题,这些子表达式树可以根据它们各自的适应度单独选择(例如,在具有多个输出的问题中),或者它们可以形成一个更复杂的多亚基表达式树,其中各个子表达式树通过某种特定的翻译后相互作用或连接相互作用。例如,代数子表达式树可以通过加法或乘法连接,而布尔子表达式树可以通过OR、AND或if(x,y,z)连接。因此,对于每个问题,连接函数的类型以及基因的数量和每个基因的长度都是先验选择的。在尝试解决问题时,我们总是可以从使用单基因染色体开始,然后逐步增加头部长度。如果头部变得非常大,我们可以增加基因的数量,并且显然选择一个函数来连接子ET。
例如:5个输入项:水灰比(w/c)、测试龄期(TA)、细骨料含量(FA)、粗骨料含量(CA)和减水剂含量(SP);1个输出项:混凝土的Dnssm数学表达式。
数学表达式按照从表达树左下角节点开始向树的右侧进行结合输出表达式(二叉树中序(左根右)输出)。
$$Dnssm=\frac{FA\times CA}{w/c+SP}$$
演化迭代过程中需要使用基因算子包括:突变、交叉、复制,对结果进行提升。
优化目标是适应度函数$f_i=\sum_{j=1}^C(M-|C_{(i,j)}-T_j|)$
- 个体$i$是第$i$ 个染色体序列, 适应度案例$j$是终止符使用的第$j$个数值。
- $C_{(i,j)}$是个体$i$在第$j$个适应度案例上的返回值(即程序运行后的输出)。
- M: 表示选择范围 (range of selection),是一个预设的常数。它代表了每个适应度案例可能贡献的最大适应度值,用于将误差转换为适应度分数。
- C: 表示适应度案例 (fitness cases) 的总数。适应度案例是用于评估程序性能的输入-输出对数据集。
- $T_j$: 表示第 j个适应度案例的目标值 (target value) 或真实值。
突变随机选择一个节点进行突变
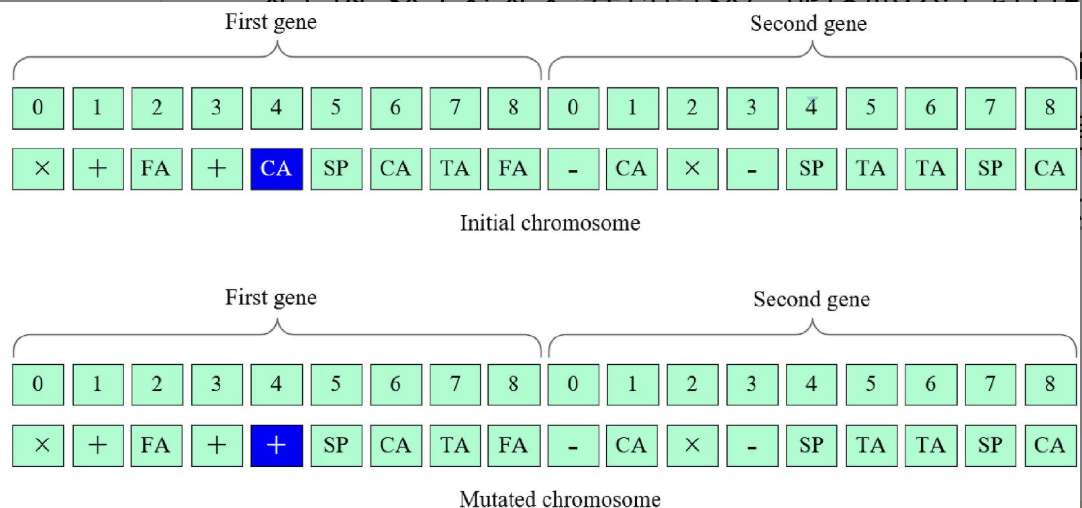
**Artificial Bee Colony Expression Programming **
-
ABCO (artificial bee colony optimization)
-
受蜜蜂寻找食物来源启发,蜜蜂分为:采蜜蜂(开发食物来源)、观察蜂(决定食物来源的质量)和侦查蜂(寻找新的食物来源)。
-
优化问题等价于觅食过程。
-
每个可能的解等价于每个食物来源。
-
目标值等价于食物质量。
-
侦查蜂随机生成一组可能的解。
-
$X_{ij}=X^j_{\min}+\mathrm{rand}(0,1)(X^j_\max-X^j_\min)$
侦查蜂给出的随机解$X_i$表示第i个食物来源,其第j特征维度的值为$X_{ij}$, j维度上的上下限$X^j_\max,X^j_\min$。
-
$X_{ij}^N=X_{ij}+\varnothing_{ij}(X_{ij}-X_{kj})$
采蜜蜂在$X_{ij}$解(分配给采蜜蜂的解)附近搜索邻域解$X_{ij}^N$, $\varnothing_{ij}$是-1到1的随机量,$X_{kj}$是一个从可能的解中(处去第i个可能解)随机选择的第k个可能解。
-
贪婪选择,当$X_{ij}^N$的目标值优于$X_{ij}$则用$X_{ij}^N$替换$X_{ij}$。给一搜索限定值,即一个采蜜蜂在$X_{ij}$的附近连续未成功搜索到邻域解$X_{ij}^N$的最大次数。
-
一旦采蜜蜂搜索次数超过限定值,则采蜜蜂转化为侦查蜂,离开食物源(解$X_{ij}$)。
-
在蜂巢中采蜜蜂和观察蜂分享食物源(可能解)的信息(食物源概率分布),每只观察蜂基于轮盘赌选择机制选择一个食物源。这里食物源的质量是一个概率分布函数,质量越高越有可能被观察蜂选中,选中的食物源的索引号即上文中的k。观察蜂选择食物源即分配的食物源后转化为采蜜蜂。
-
-
ABCP (artificial bee colony programming)
-
每个食物源都由一个具有树状结构的计算机程序(函数)表示。
-
为了生成食物源$F_1$的邻域解$F_n$,随机选择F1的一个子树,并用食物源$F_2$的一个随机子树替换。食物源$F_2$是观察蜂使用轮盘赌选择机制从可用的食物源中随机选择。
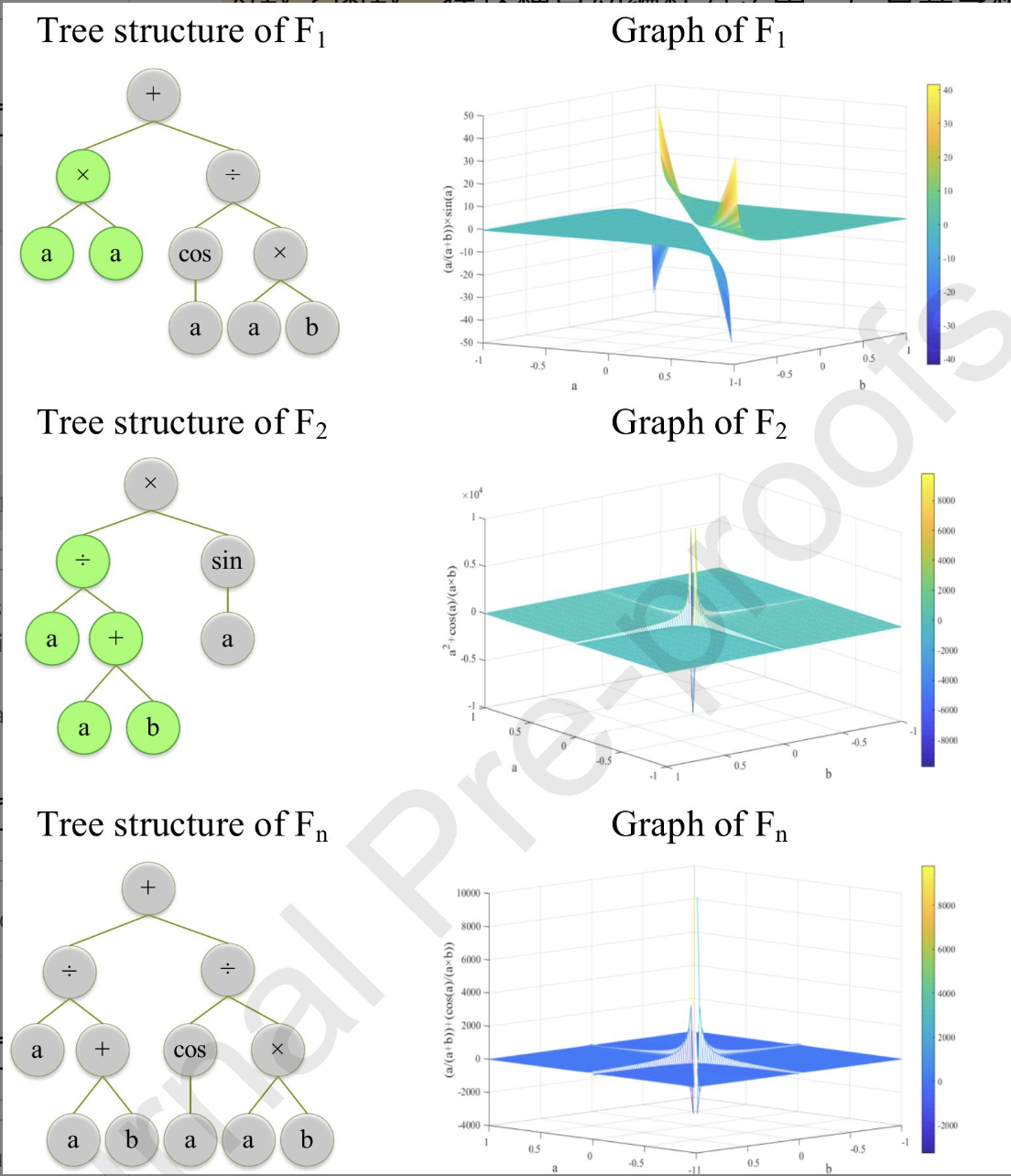
-
-
ABCEP (artificial bee colony expression programming)
-
食物来源候选者(可能的解决方案)被定义为具有固定长度的线性字符串。这些线性字符串可以很容易地转换为非线性实体,表示具有不同形状和大小的表达式树。
-
ABCP中特殊树的改变是通过子树的替换发生的,这可能导致出现更复杂的树。在表达式编程中,树的每个节点都可以独立改变,从而缓解了ABCP中偏离答案的问题。
-
不同的算子会影响GEP中的表达式,这可能会以产生非理性结果的方式改变表达式。例如,如果一个单一表达式通过反转、突变、插入序列、根插入序列和其他算子依次改变,则很可能出现无关紧要的表达式。
-
在ABCEP中,单个表达式通过一种称为表达式共享的简单机制来改变。如果在确定的世代中没有找到合适的表达式,搜索次数限制会阻止无用的搜索,并开始新的搜索,直到系统检测到好的结果。
-
每个食物来源都有一个头部,包含函数、变量和常量,以及一个尾部,仅包含变量和常量(GEP定义))。函数可以包括算术运算(+、-、÷、×)、数学函数(sin、cos、exp、log)、编程运算、逻辑函数或特定领域的函数。
-
生成初始解:每个解(食物来源)都是一个表示为线性字符串的数学公式,并且初始解是随机创建的。在运行算法之前,需要指定使用的函数、头大小、每个函数的参数数量、最大迭代次数(或节点函数评估)、解的数量、采蜜蜂和观察蜂的数量以及邻域搜索次数最大值。
-
评估解的质量:使用适应度函数衡量每种食物来源的质量。
-
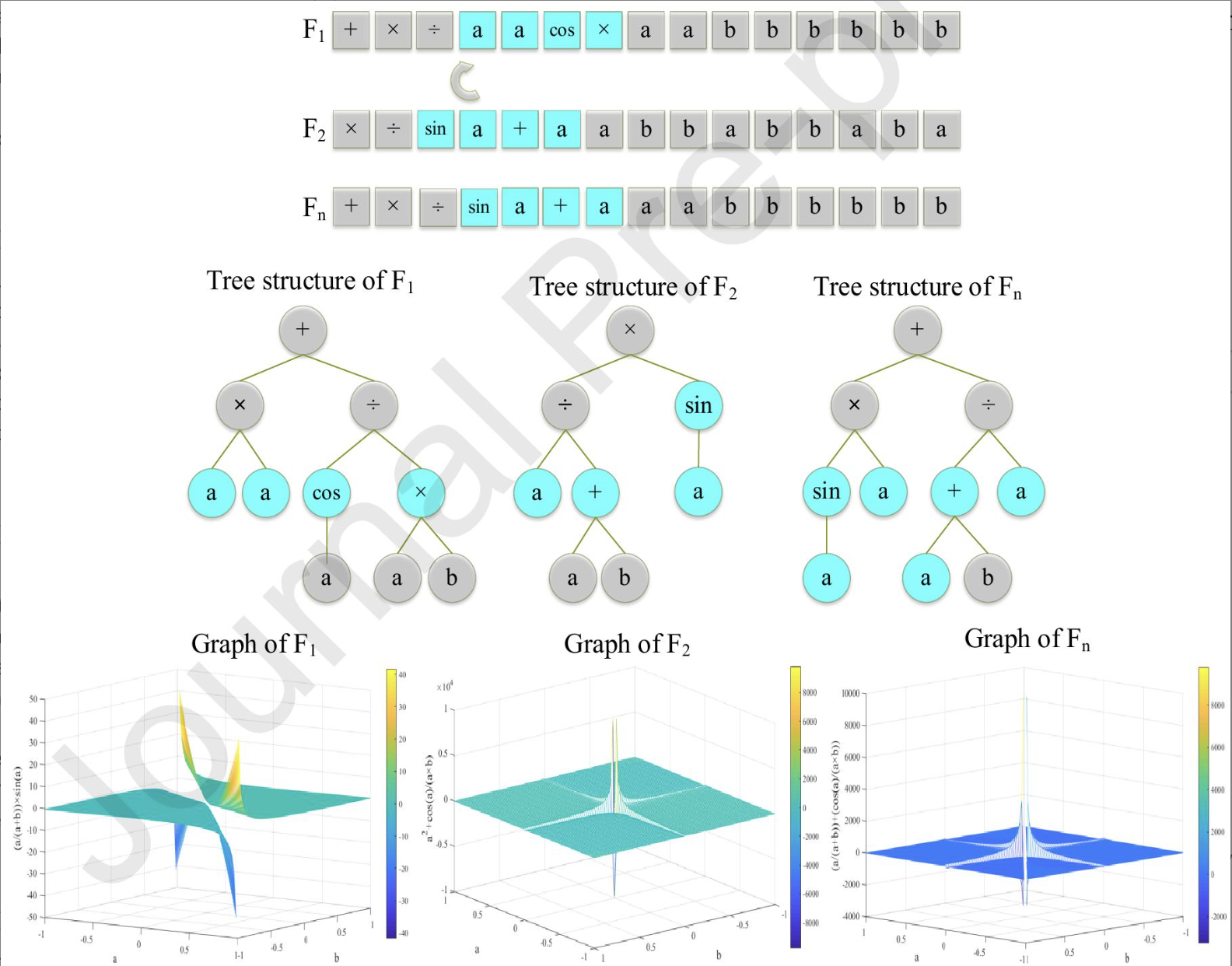
使用采蜜蜂搜索当前解决方案的邻域解决方案:采蜜蜂通过表达式共享机制搜索所有表达式解的邻域。对于表达式解 $F_1$,无论其质量如何,都会在可用的表达式解中随机选择一个表达式解 $F_2$。然后,将 $F_1$ 的一个子表达式替换为 $F_2$ 的一个子表达式,以创建$F_1$ 的一个邻域表达式解,标记为 $F_n$。
- $F_1$和$F_2$子表达式的长度必须一样,子表达式的**起点(第一个点)**的选择分为函数和终端符号,以 ω 的概率在相关字符串头部中选择函数,以 1-ω 的概率在相关字符串中选择终端符号。
- 如果选定的函数之后只有终端符号(变量和常量),那么将随机选择其中之一作为子表达式的第二个点。这意味着在确定了第一个点(特别是函数节点)之后,算法会根据子表达式长度相等的原则,继续选择第二个点来界定整个子表达式的范围。
-
贪婪选择机制:用适应度函数评估邻域解$F_n$的质量,如果邻域解$F_n$的质量由于$F_1$,则用$F_n$替换$F_1$。否则搜索失败一次,如果连续搜索失败的次数超过搜索次数最大值,则采蜜蜂放弃食物源$F_1$转为侦查蜂寻找新食物源。(避免局部最优解)
-
确定概率分布函数:当采蜜蜂开发搜索完所有食物源的邻域后,根据如下公式为所有食物源分配一个概率分布函数。
$$p_i=\frac{0.9\times fit_i}{fit_{best}}+0.1$$
$$fit_i=\frac{1}{1+C_i}$$
$$C_i=\sum_{j=1}^N|T_j-P_{ij}|$$
这里$C_i$,$fit_i$是第i个食物源的成本(误差值)和适应度值,$fit_{best}$ 是所有食物源中的最佳适应度值,$p_i$是食物源i的选择概率,N是案例数量(即属性数、特征数),$T_j$是第j个案例的目标值(真实值),$P_{ij}$是第i个食物源(解决方案)对第j个案例(特征)的预测输出值。
-
使用观察蜂开发当前解决方案:观察蜂和采蜜蜂共享信息(食物源概率分布),观察蜂根据概率分布选择一个食物源(表达式解)作为上文中的$F_2$用于计算表达式解$F_1$ 的邻域表达式解$F_n$,观察蜂转为采蜜蜂。
-
保存最佳解:在每次迭代结束时,保存本次迭代获得的最佳公式,并且可以在整个迭代过程中绘制误差值。
-
算法的终止条件:不断搜索新的食物来源,直到满足ABCEP算法的终止条件,即如果所有生成的公式的累积节点数高于预定义的阈值,算法将停止。不是指当前种群中所有程序的节点总数,而是指算法在整个运行过程中,所有曾经被创建、修改过的程序的节点数的总和。
-
-
5、相关研究:
6、指标:
7、分析:
8、改进:
Robustness Analysis Based on Optical FiberSensor Networks Topology
1、研究目标:改良评估网络鲁棒性的模型,基于蒙特卡洛方法提出鲁棒性的误差评估。
2、难点:缺少定量评估网络鲁棒性的方法
3、背景:
- 传感网络$M$的鲁棒性由网络检测的覆盖率的数学期望表示。
- 光纤传感器的检测能力由指数函数表示$f(\vec{r}_q)=e^{-\alpha\vert\vec{r}_q-\vec{r}_s\vert}$, 衰减系数由传感器的类型决定。
- 整个网络的检测能力表示为$f(\vec{r}q)=1-\prod\limits{i=1}^n (1-e^{-\alpha_i\vert\vec{r}_q-\vec{r}_s\vert}\times W_i)$, $W_i$是传感器状态,第i个传感器正常工作$W_i=1$否则为0。
- 传感器的网络的工作状态表示为$\vec{M}k=(W_n,W{n-1},\cdots,W_1)$,用十进制数k表示二进制向量$k=1+\sum\limits_{i=1}^{n}2^{i-1}*W_i$
- 阈值$\gamma$评估是否传感器网络$M$是否有效检测到Q点$H(\vec{r}_q)=\begin{cases}1 & f(\vec{r}_q)\ge\gamma \ 0 & f(\vec{r}_q)<\gamma\end{cases}$
- 网络状态为$k$时对区域$R$的网络检测覆盖率$A_k(\vec{r})=\int_RH_k(\vec{r})d\vec{r}/\int_Rd\vec{r}$
- 网络$M$的鲁棒性$U=\sum\limits_{k=1}^{2^n}A_k(\vec{r})\cdot P(\vec{M}_k)$, $P(\vec{M}_k)$是网络状态为$k$时发生的几率。
4、方法:
误差分析方法
-
采样大小$m$,第i次采样点的网络检测能力$f(\vec{r}_i)(i=1,2,\cdots,m)$
-
统计检测能力$f(\vec{r})$大于阈值$\gamma$的采样点数$\sum\limits_{i=1}^mH(\vec{r}_i)$
-
蒙特卡洛估计的网络在$k$状态下的覆盖率$A_k(\vec{r}i)=A_e=(\sum\limits{i=1}^mH(\vec{r}_i))/m$
-
$H(\vec{r}_i)$服从伯努利分布(二项分布)$\mathrm{B}(m,A_k)$, 在$\vec{r}_i$采样点处的均值$\mu=A_k$,方差$\sigma^2=A_k\times(1-A_k)$
-
中心极限定理,大量的$H(\vec{r}i)$采样后求和函数服从正态分布$\mathcal{N}(\mu,\sigma^2/m)$,标准化后$(\sum\limits{i=1}^mH(\vec{r}_i)-m\cdot A_k)/\sqrt{m\cdot A_k(1-A_k)})\sim\mathcal{N}(0,1)$
-
$-z_{\partial/2}\lt(m\cdot A_e-m\cdot A_k)/\sqrt{m\cdot A_k(1-A_k)}\lt z_{\partial/2}$
$\vert (m\cdot A_e-m\cdot A_k)/\sqrt{m\cdot A_k(1-A_k)} \vert\lt z_{\partial/2}$
$\vert (m\cdot A_e-m\cdot A_k)/\sqrt{m\cdot A_k(1-A_k)} \vert^2\lt z^2_{\partial/2}$
支持向量机
评估传感器的检测能力$f(\vec{r}_q)=e^{-\alpha\vert\vec{r}_q-\vec{r}_s\vert}$
- 任务:预测目标点温度
- 温度计在加热点测量实际温度,传感网络在数据点收集应变数据。
- 以传感网络收集数据作为支持向量机的输入,输出预测的温度
- 训练/测试:训练:学习应变到温度的映射关系,测试:学习后预测的准确性
- 检测能力的指标:$f=1/\sqrt{mse}$, 预测值与真实值之间的均方误差。
计算衰减系数和阈值
衰减系数:
- 选择一个传感器,例如位置在(65,50)。
- 设置检测位置目标点, 例如(50, 50)。
- 收集目标点的温度数据一共45组。
- 数据划分,35组用于支持向量机训练,10组用于测试。
- SVM的预测和实际温度之间的均方误差给出传感器的检测能力$f=1/\sqrt{mse}$。
- 根据传感器的检测能力公式计算衰减系数$\alpha$。
阈值:
- 逐步增加传感器数量,计算网络的鲁棒性或覆盖率。
- 当覆盖率或鲁棒性饱和时的传感器数量作为计算网络有效阈值的传感器的数量。
- 收集加热目标点的温度数据和每个传感器的应变数据。
- 利用SVM预测值计算每个传感器的检测能力。
- 使用计算的检测能力和饱和的覆盖率计算阈值$\gamma$。
5、相关研究:
6、指标:
7、分析:
8、改进:




