1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
模版
1、研究目标：

2、难点：

3、背景：

4、方法：

5、相关研究：

6、指标：

7、分析：

8、改进：

深度预测-----------------------------------------------------------------------

Depth Map Prediction from a Single Image using a Multi-Scale Deep Network

1、研究目标：预测三维几何结构深度。

2、难点：

  • finding depth relations from a single image is less straightforward, requiring integration of both global and local information from various cues.
  • 深度预测本身具有模糊性、技术上 不适定（一个没有唯一、稳定或存在解的问题），全局尺度问题（正常房屋和玩具屋），将注意力集中在场景内的空间关系而不是场景尺度上。

3、背景：

  • 深度估计的需要的图像线索包括：线条角度和透视、物体大小、图像位置和大气效应。

4、方法：

  • 通过采用两个深度网络堆栈来解决此任务：一个基于整个图像进行粗略的全局预测，另一个在局部细化此预测。

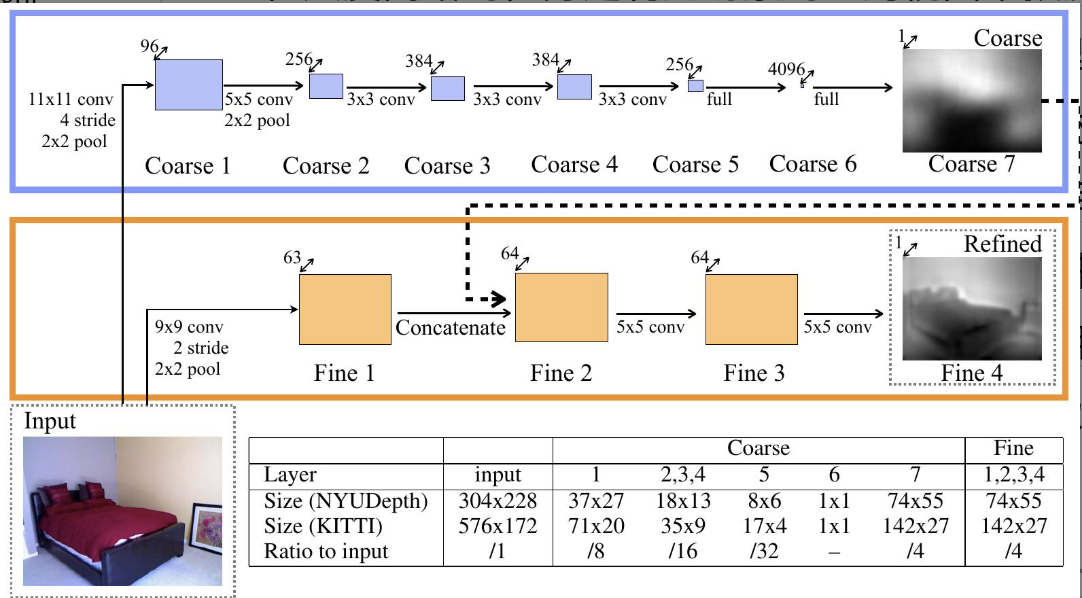
    image-20251027090655478

  • 场景内使用尺度相关误差，整个场景使用尺度不变误差。

    • 使用一个预言机将每个预测的平均对数深度替换为来自相应真实值的平均值，可将误差降低至0.33，相对提高了20%。

    • 一个预测深度图y和一个真实深度图$y^*$，每一个都有n个像素，以i为像素索引，定义尺度不变均方误差为：

      $$D(y,y*) = \frac{1}{2n}\sum_{i=1}^n(\log y_i-\log y^_i+\alpha(y,y^))^2$$

      $$\alpha(y, y^) = \frac{1}{n}\sum_i(\log y_i^-\log y_i)$$​

    • $e^\alpha$是对齐预测图和真实图的最佳尺度。使得缩放y图具有相同的误差。

    • 等价公式, 定义$d_i = \log y_i - \log y_i^*$

      $$D(y,y^) = \frac{1}{2n^2}\sum_{i,j}((\log y_i-\log y_j)-(\log y_i^-\log y_j^*))^2$$

      $$= \frac{1}{2n^2}\sum_{i,j}(d_i-d_j)^2$$​​

      $$= \frac{1}{n}\sum_i d_i^2 - \frac{1}{n^2}\sum_{i,j}d_id_j = \frac{1}{n}\sum_id_i^2-\frac{1}{n^2}(\sum_id_i)^2$$

      为了使误差较低，预测中每对像素的深度差异必须与ground truth中相应像素对的深度差异相似

  • 损失值除了考虑逐点误差，还考虑像素间深度关系。

    • $$L(y,y^*)=\frac{1}{n}\sum_id^2_i-\frac{\lambda}{n^2}(\sum_id_i)^2$$​

  • 处理在目标边界、特殊表面上的缺失值

    • 只处理有效点位，屏蔽掉缺失值，即计算损失值的点位值考虑有效点位。

  • 图像预处理：

    • 图像缩放：输入和目标图像按比例因子 s ∈ [1, 1.5] 缩放，深度值除以 s。
    • 旋转：输入和目标旋转 r ∈ [−5, 5] 度。
    • 裁剪：输入和目标被随机裁剪
    • 颜色：输入值全局乘以一个随机RGB值c ∈ [0.8, 1.2]
    • 以0.5的概率水平翻转：输入和目标在水平方向上翻转

  • 图像分辨率扩展：

    • 使用最近邻插值将预测结果上采样到完整的原始输入分辨率。

5、相关研究：

  • A. Saxena, S. H. Chung, and A. Y. Ng. Learning depth from single monocular images. In NIPS, 2005.
    • 1、依赖图像水平对齐，2、在较少受控环境中表现不好。
  • M. P. Lubor Ladicky, Jianbo Shi. Pulling things out of perspective. In CVPR, 2014.
    • 1、依赖手工特征，2、超像素分割图像。
  • C. Liu, J. Yuen, A. Torralba, J. Sivic, and W. Freeman. Sift flow: dense correspondence across difference scenes. 2008.
    • 1、运行时需要整个数据集，2、对齐程序执行成本高。
  • K. Konda and R. Memisevic. Unsupervised learning of depth and motion. In arXiv:1312.3429v2, 2013.
    • 1、依赖立体视觉提供的局部位移。

6、指标：

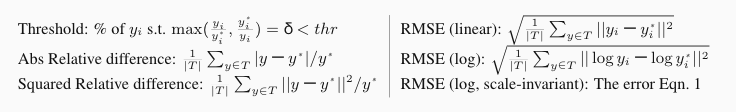
image-20251027141824713

7、分析：

  • 当网络在这样的数据上进行训练时，由于边缘位置的不一致性，网络会倾向于**平均化（average over their more random placements）**这些随机错位的边缘位置。这种平均化效应导致预测的深度图在这些区域的边缘过渡变得模糊，无法像预期的那样实现锐利的细节对齐。因此，尽管模型在整体上可能表现良好，但在精细的局部结构（如物体边界和墙壁边缘）的预测上仍可能存在不足。
  • 虽然精细尺度网络在误差测量方面没有改进，但其效果在深度图中清晰可见——表面边界具有更清晰的过渡，与局部细节对齐。
  • We achieve a new state-of-the-art on this task，having effectively leveraged the full raw data distributions.

8、改进：

  • 兼容3D几何信息，例如表面法线。
  • extend the depth maps to the full original input resolution by repeated application of successively finer-scaled local networks.

扩散---------------------------------------------------------------------------------------

DiffusionDepth: Diffusion Denoising Approach for Monocular Depth Estimation

GitHub

1、研究目标：

一种将单目深度估计重新定义为去噪扩散过程的新方法。

2、难点：

  • 回归类方法会遭受过拟合和不能令人满意的目标细节问题。

  • 二维图片和三维场景间映射的内在模糊性。

  • 离散的深度值会导致图像质量降低，体现在图像不连续和模糊。

  • Q: 生成方法产生深度预测的问题是稀疏的真实深度图。该问题会使模型在正常的生成训练过程中崩溃。

    A: 引入自扩散过程，取代对真实深度图的直接扩散，逐渐向从当前的去噪图中优化的潜藏深度表示添加噪声。

3、背景：

autonomous driving, robotics, and augmented reality

4、方法：

  • 迭代去噪过程即从随机深度分布图中生成深度图。从左到右是去噪优化过程，从右到左是扩散过程。

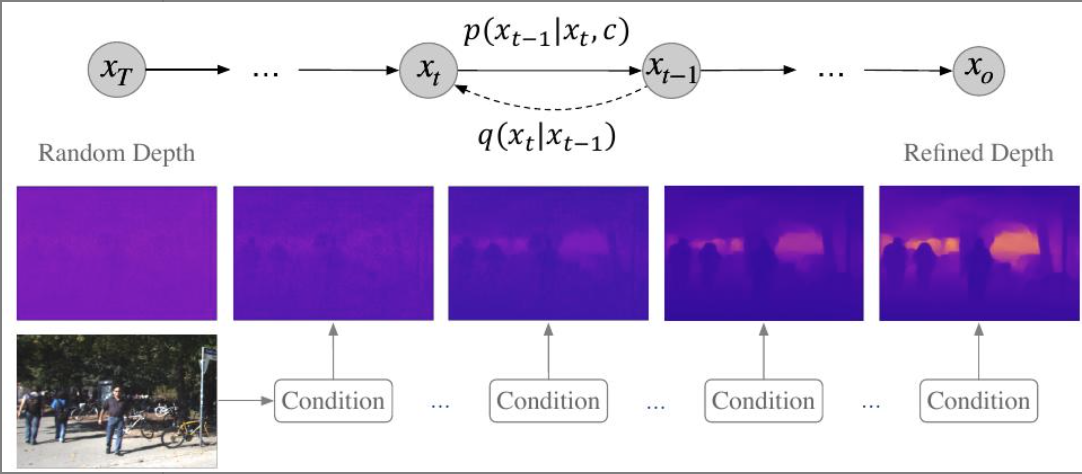
image-20251102162749127

  1. 扩散过程：$$q(x_t|x_0) := N(\bold{x}_t|\sqrt{\bar{\alpha_t}}\bold{x}_0, (1-\bar{\alpha_t})I)$$，即对图像进行高斯噪声模糊，迭代式向期望的深度图像分布$\bold{x}_0$添加噪声，并在添加t次噪声后得到潜在深度图的噪声样本$\bold{x}t$, $t\in{0,1,\cdots,T}$, 其中$\bar{\alpha}t:=\Pi{s=0}^t\alpha_s=\Pi{s=0}^t(1-\beta_s)$而$\beta_s$表示在s步上添加噪声的方差, $\bar{\alpha}_t$是一个随时间步 t 变化的系数，控制着原始信号的强度。，$(1-\bar{\alpha_t})I$协方差矩阵,$I$是单位矩阵，表示噪声是各向同性的（即在所有维度上的方差都相同）, $1-\bar{\alpha_t}$是一个随时间步 t变化的系数，控制着噪声的强度。

  2. 去噪过程: $$p_\theta(\bold{x}{t-1}|\bold{x}t):=N(\bold{x}{t-1};\mu\theta(\bold{x}t,t), \sigma^2_tI)$$，训练神经网络$\mu\theta(\bold{x}t,t)$通过交互式预测$\bold{x}{t-1}$返回到$\bold{x}_0$。其中$\sigma_t^2$表示转移方差。期望的样本$\bold{x}_0$是从先验噪声$\bold{x}_T$​通过数学推理过程重构的。

  3. 通过给定的图像特征图$\bold{c}\in\mathbb{R}^{\frac{H}{4}\times\frac{W}{4}\times C}$引导的去噪过程：$$p_\theta(\bold{x}{t-1}|\bold{x}t,\bold{c}):=N(\bold{x}{t-1};\mu\theta(\bold{x}_t,t,\bold{c}), \sigma^2_tI)$$

  • 提取随机深度分布作为输入，借助视觉图片引导通过去噪步骤精炼优化深度分布图，深度潜藏层由编解码器构成。通过稀疏有效屏蔽掩码在深度潜藏空间和深度图像空间分别对齐优化的深度预测和稀疏真实值。在许多深度估计数据集中，特别是室外场景（如KITTI），真实深度值往往是稀疏的，即并非所有像素都有对应的真实深度标注。稀疏有效掩码的作用是指示哪些像素点具有可用的真实深度值，从而确保损失函数只在这些有标签的有效像素上计算，避免模型被无标签区域的噪声或不确定性所误导。通过这种方式，模型能够有效地从稀疏的真实深度数据中学习，并将精炼后的预测深度与这些有限但准确的真实值进行对齐，从而克服了在稀疏GT场景下训练生成模型的挑战。

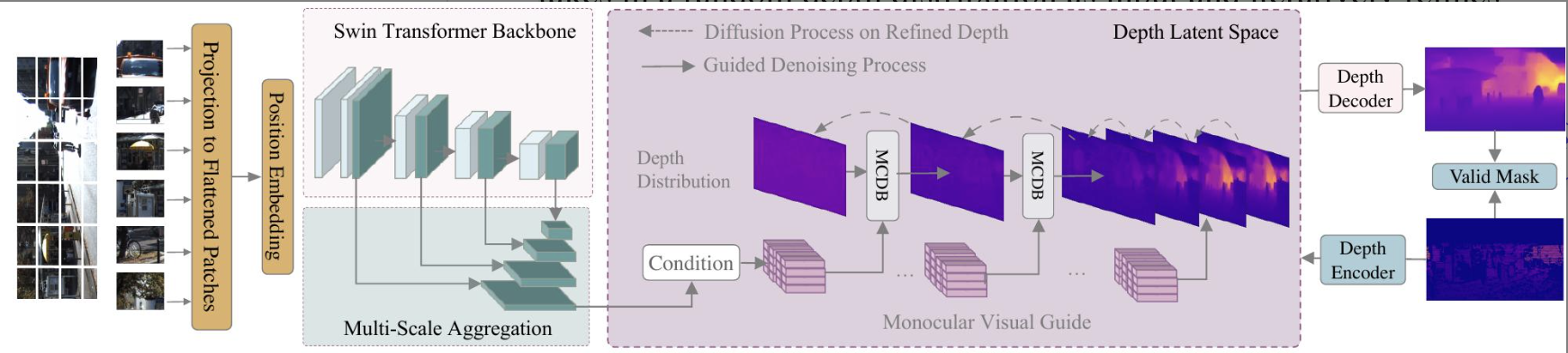
image-20251102164307115

Swin Transformer提取特征，输入的图像先分块，再映射成视觉词牌向量并添加位置嵌入向量。提取特征过程分别对不同尺度的图形进行。将不同尺度的特征聚合成$\frac{H}{4}\times\frac{W}{4}\times c$​​的特征。

潜藏空间

  1. 不论扩散过程还是去噪过程使用的潜藏深度图,真实$\hat{x}_0\in\mathbb{R}^{\frac{H}{2}\times\frac{W}{2}\times d}$是通过对真实深度图$\hat{de}\in\mathbb{R}^{H\times W\times 1}$编码得到的, 其中潜藏维度为$d$​。

    编码过程使用具有$d$个通道、卷积核大小为1x1的瓶颈卷积模块。

  2. 提炼到的潜藏深度图$x_0\in\mathbb{R}^{\frac{H}{2}\times\frac{W}{2}\times d}$到预测的深度图$de\in\mathbb{R}^{H\times W\times 1}$的解码过程是由1x1卷积、3x3反卷积、3x3卷积和Simoid激活函数依次连接构成，其中潜藏维度为$d$。深度图的计算公式为$de=(\frac{1}{sig(x_0)}).clamp(\eta)-1$, $\eta$是最大输出深度的范围$1\mathrm{e}^6$。

  3. 优化潜藏空间损失函数（双重监督）

    • 深度图的损失$$L_{pixel}=\sqrt{\frac{1}{T}\sum_i\delta_i^2+\frac{\lambda}{T^2}(\sum_i\delta_i)^2}$$​

      $$\delta_i=\hat{de}-de$$是在有效掩码屏蔽后的真实深度图像和预测的深度图像逐像素的差值，$T$​​是所有有效的像素数目（有效屏蔽掩码未屏蔽的像素）。

    • 深度潜藏图的损失$L_{latent}=||x_0-\hat{x}_0||^2$，屏蔽掩码需要下采样到和深度潜藏图同尺度再进行屏蔽。

  • MCBD (Monocular Conditioned Denosing Block)

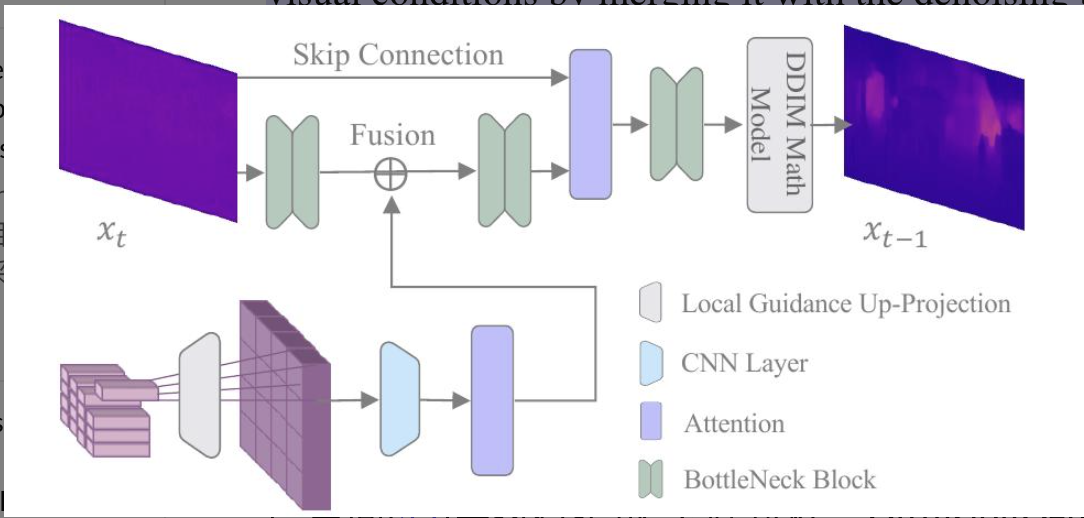
    image-20251102165651811

$\mu_\theta(\bold{x}_t,t,C)$的实现过程由MCBD描述。$C$是低分辨率的特征图像，与需要被去噪的深度潜藏图像$x_t$有局部强相关性。

  1. 对$C$做投影（转置卷积）实现上采样使它和深度潜藏图$x_t$有相同的空间尺度和特征尺度$x_t\in\mathbb{R}^{\frac{H}{2}\times\frac{W}{2}\times d}$​同时保持局部相关性。
  2. 对投影的特征图做卷积和自注意力处理。
  3. 将自注意力处理后的投影特征图与经常规瓶颈网络处理后的深度潜藏图做对应像素相加式融合。
  4. 融合后的深度潜藏图在被常规瓶颈网络处理、被带有残差连接的通道注意力网络处理。
  5. 上述输出的深度潜藏图再经DDIM处理，预设好扩散超参$\beta,\alpha$​。

损失函数

扩散-去噪过程中可训练的参数在$$\mu_\theta(\bold{x}t,t,C)$$和视觉特征提取过程中。优化过程是最小化扩散结果和去噪预测之间的损失值，即去噪损失$$L{ddim}=||x_{t-1}-\mu_\theta(\bold{x}_t,t,C)||$$​​。

总的损失函数为$$L=\lambda_1L_{ddim}+\lambda_2L_{pixel}+\lambda_3L_{latent}$$。

5、相关研究：

  • cnn
    • Depth map prediction from a single image using a multi-scale deep network
    • Deep ordinal regression network for monocular depth estimation
  • diffusion
    • Denoising diffusion probabilistic models
    • Score-based generative modeling through stochastic differential equations
    • Diffusion models beat gans on image synthesis

6、指标：

  • 尺度不变对数误差（SILog）的平方根

image-20251104200543551

  • 均方根对数误差 (RMS log)

    $\frac{1}{N}\sqrt{\sum_{i,j}(e^{i,j})^2}$​

  • 域值精度($\delta_k$)：满足$\max(\frac{\hat{X}^{i,j}}{Z_{gt}^{i,j}}, \frac{Z_{gt}^{i,j}}{\hat{X}^{i,j}})<1.25^k$的$\hat{X}^{i,j}$的百分比

7、分析：

8、改进：

超分辨-------------------------------------------

Deep Depth Super-Resolution : Learning Depth Super-Resolution using Deep Convolutional Neural Network

1、目标：

基于深度卷积神经网络在彩色图像超分辨率方面的成功，我们提出了一种基于深度神经网络的深度图像超分辨率方法，以有效地学习从低分辨率深度图像到高分辨率深度图像的非线性映射。

2、难点：

  • 下采样图像丢失信息, LR图像中的已知变量远远少于HR深度图像中的未知变量。

  • 彩色图像和深度图像的本质差别

    • 信息获取机制：彩图捕捉物体表面光照、颜色、纹理；深图记录传感器距离信息。
    • 梯度特性：深图具有更少的纹理和锐利边界；
    • 高频信息敏感度：彩图高频信息包含：纹理、边界；深图高频信息包含：边界、几何结构变化非纹理，其精细结构易受噪声影响。

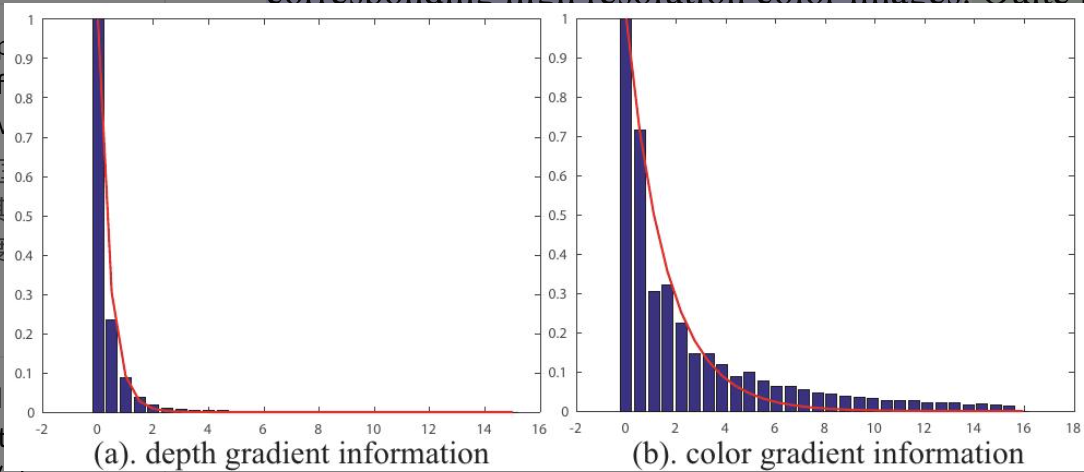
    image-20251027193801176

  • 当模型应用于具有不同RGB-D统计特性的新场景或数据集时，其生成的深度图像可能出现偏差（biased)。这种偏差可能表现为重建细节失真、边缘不准确或对噪声过于敏感等问题。做平滑处理。

    image-20251028192850609

3、背景：

  • depth cameras，time-of-flight (ToF) cameras，computer graphics，3D modeling，computer interaction.
  • inferring all the missing high frequency contents.

4、方法：

  • 提出了一种渐进式深度CNN框架，用于从低分辨率深度图像逐步学习高分辨率深度图像。
  • 利用深度场统计，深度图像与彩色图像之间的局部相关性提升细节；将先验知识整合到一个能量最小化公式中，深度神经网络学习一元项，深度场统计作为全局模型约束以及颜色-深度相关性用于加强深度图像中的局部结构。
    • 条件随机场（conditional random field）。
    • 能量最小化框架由一元项、全局约束项、局部结构约束项。
    • 一元项：直接依赖于单个像素或单个数据点自身特征的能量项（置信度、初始估计）
  • 对于没有高分辨率彩色图像的深度图像，深度图像本身可以被用来优化深度图像。
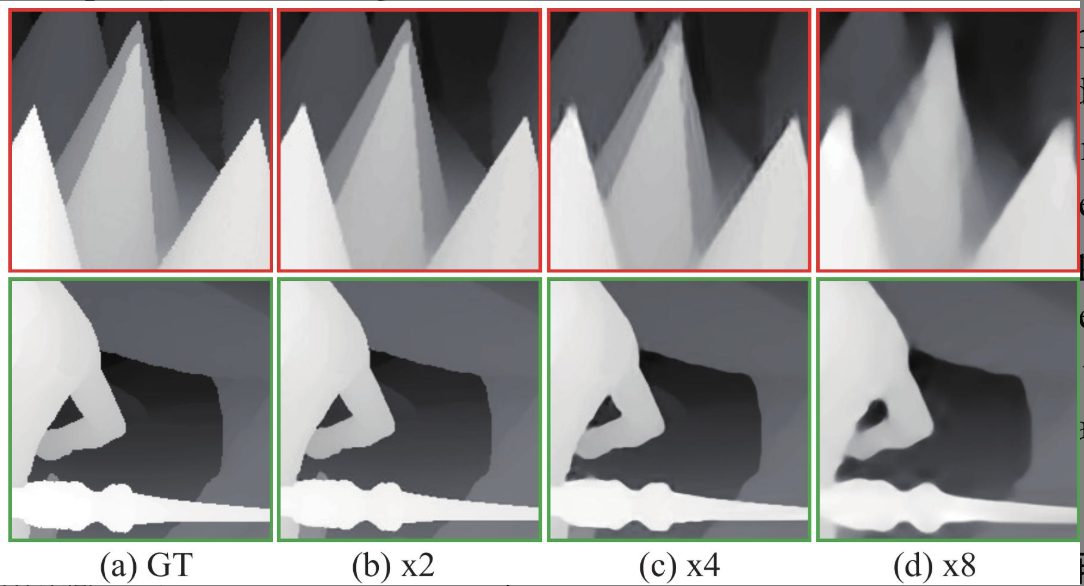
  • 高分辨深图$D^H$和低分辩深图$D^L$, 从低分辩到高分辨的映射函数$F$​​由深度神经网络表示。上采样因子取值范围x2,x4,x8，

渐进卷积神经网络

  • 渐进过程指多个计算深度图超分辨的卷积神经网络单元，每一个单元将前一个低分辩深图$D_i^L$计算出高分辨深图$D_{i+1}^L$，其作为下一个计算单元的低分辩深图输入。

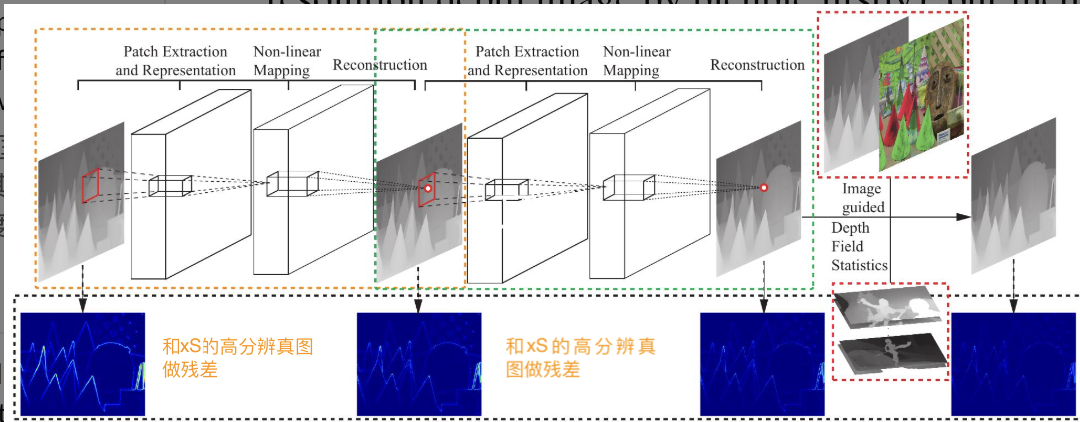
image-20251027210144677

  • 每一个神经网络计算单元参考Image Super-Resolution Using Deep Convolutional Networks。
  • 原则上可以训练整个网络，为了便于训练，连续训练每一个单元。
  • 提取表示层使用64个卷积核大小9x9；非线性层使用32个卷积核大小1x1;重构层使用卷积核大小5x5

颜色调制

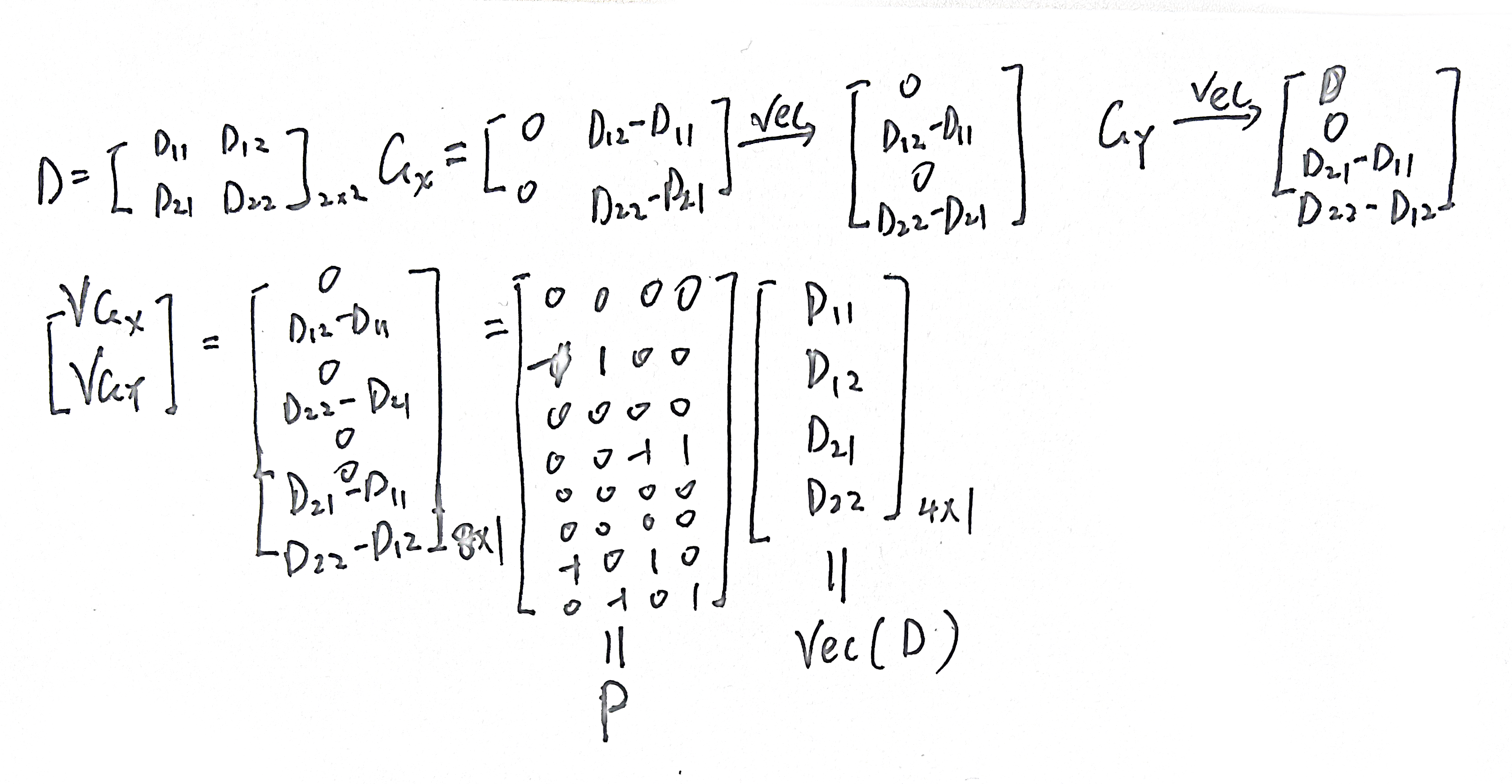
记深度图像$u$位置的深度值为$D_u$, 颜色调制的推理模型可以表达为

$$D_u=\sum_{v\in\Theta_u}\alpha(u,v)D_v$$

其中$\Theta_u$是像素$u$的邻域。调制的模型和深度图在位置$u$的差异表示为

$$\psi_u(D_u) = (D_u^*-\sum_{v\in\Theta_u}\alpha(u,v)D_v)^2$$​

在整个深度图像上的差异表示为（卷积的矩阵表达）

$$\sum_u\psi_u(D_u)=||A\mathrm{vec}(D)-\vec{b}||^2$$​

设计像素u附近邻域的$\alpha(u,v)$时既要引入已有的高分辨颜色图像又要考虑对应的卷积网络预测的高分辨深度图像。

$$\alpha(u,v) = \frac{1}{N_u}\alpha^{D^*}(u,v)\alpha^I(u,v)$$​

$$\alpha^{D^}(u,v)\propto\exp(-(D^_u-D^v)^2/2\sigma^2{D_u^})$$​

$$\alpha^{I}(u,v)\propto\exp(-(I_u-I_v)^2/2\sigma^2_{I_u})$$​

其中$N_u$是归一化因子，I是高分辨彩图，$\sigma_\cdot$是像素$u$​邻域内的方差。邻域大小为7x7,如果没有深度图对应的彩图就只使用深度图。

深度场统计

深度场梯度近似服从Laplace distribution，有一个2SHSWxSHSW矩阵P用于提取图像的X和Y方向的梯度，最小化总变差$||D||{TV}\rightarrow \min$, $||D||{TV}=||P\mathrm{vec}(D)||_1$​

WechatIMG46 拷贝

最小化能量公式

$$\min_D\frac{1}{2}||D-D^*||^2_F+\lambda_1||A\mathrm{vec}(D)-\vec{b}||^2+\lambda_2||P\mathrm{vec}(D)||_1$$

$||\cdot||_F$ Frobenius 范数定义为矩阵元素的平方和的平方根。$\lambda_1, \lambda_2$取0.7，根据$P$提取的方向改写公式：

$$\min_D\frac{1}{2}||D-D^*||^2_F+\lambda_1||A\mathrm{vec}(D)-\vec{b}||^2+\lambda_2\sum_i||P_i\mathrm{vec}(D)||_1\quad i\in{X,Y}$$

参数$A,\vec{b},P$是深度图计算得到的参量而非优化目标直接更新的参量。

优化方法：IRLS（iterative reweighted least squares）,给定第it次迭代中的深度图估计结果$D^{(\mathrm{it})}$，第it+1次迭代时优化表示为

$$\min_D\frac{1}{2}||D-D^*||^2_F+\lambda_1||A\mathrm{vec}(D)-\vec{b}||^2+\lambda_2\sum_i\frac{||P_i\mathrm{vec}(D)||^2}{||P_i\mathrm{vec}(D)^{\mathrm{it}}||}\quad i\in{X,Y}$$​

$$\rightarrow\min_D\frac{1}{2}||D-D^*||^2_F+\lambda_1||A\mathrm{vec}(D)-\vec{b}||^2+\lambda_2\sum_i||\frac{P_i}{\sqrt{||P_i\mathrm{vec(D^{(\mathrm{it})})}||}}\mathrm{vec}(D)||^2\quad i\in{X,Y}$$​

记$E_i^{(\mathrm{it})}=\frac{P_i}{\sqrt{||P_i\mathrm{vec(D^{(\mathrm{it})})}||}}$为对P每行的重权重, $E_i^{(\mathrm{it})}=\left[\begin{align*}E_X^{(\mathrm{it})}\ E_Y^{(\mathrm{it})} \end{align*}\right]$

$$D^{(\mathrm{it}+1)}=\arg,\min_D\frac{1}{2}||D-D^*||^2_F+\lambda_1||A\mathrm{vec}(D)-\vec{b}||^2+\lambda_2\sum_i||E^{(\mathrm{it})}\mathrm{vec}(D)||^2_F$$

5、相关研究：

  • 深度图超分辨方法可以分为

    • depth image super-resolution from multiple depth images，同一场景在不同时间或从略微不同视角捕获的多张低分辨率深度图像。
    • single depth image super-resolution with additional depth map data-set，仅仅一张低分辨率深度图像推断出高分辨率深度图像，为了克服单张图像信息量不足的问题，它会利用一个预先训练好的模型或一个外部的、包含大量高分辨率深度图像的数据库/数据集来提供先验知识。
    • depth image SR with the assistant of high resolution color image

  • Mac Aodha, O., Campbell, N.D., Nair, A., Brostow, G.J.: Patch based synthesis for single depth image super-resolution. In: Proc. Eur. Conf. Comp. Vis. Springer (2012) 71–84

  • Hornacek,´ M., Rhemann, C., Gelautz, M., Rother, C.: Depth super resolution by rigid body self-similarity in 3d. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. (2013) 1123–1130

  • Ferstl, D., Ruther, M., Bischof, H.: Variational depth superresolution using example-based edge representations. In: Proceedings of the IEEE International Conference on Computer Vision. (2015) 513–521

  • Xie, J., Feris, R.S., Sun, M.T.: Edge-guided single depth image super resolution. Image Processing, IEEE Transactions on 25 (2016) 428–438

  • Park, J., Kim, H., Tai, Y.W., Brown, M.S., Kweon, I.: High quality depth map upsampling for 3d-tof cameras. In: Computer Vision (ICCV), 2011 IEEE International Conference on, IEEE (2011) 1623–1630

  • Yang, J., Ye, X., Li, K., Hou, C.: Depth recovery using an adaptive

    color-guided auto-regressive model. In: Computer Vision–ECCV 2012.

    Springer (2012) 158–171

  • Ferstl, D., Reinbacher, C., Ranftl, R., Ruther, M., Bischof, H.: Image ¨

    guided depth upsampling using anisotropic total generalized variation.

    In: Proceedings of the IEEE International Conference on Computer

    Vision. (2013) 993–1000

  • Zeyde, R., Elad, M., Protter, M.: On single image scale-up using sparserepresentations. In: Curves and Surfaces. Springer (2010) 711–730

  • Yang, J., Wright, J., Huang, T.S., Ma, Y.: Image super-resolution via

    sparse representation. 19 (2010) 2861–2873

  • Timofte, R., Smet, V., Gool, L.: Anchored neighborhood regression for

    fast example-based super-resolution. In: Proc. IEEE Int. Conf. Comp.

    Vis. (2013) 1920–1927

  • Bevilacqua, M., Roumy, A., Guillemot, C., Alberi-Morel, M.L.: Lowcomplexity single-image super-resolution based on nonnegative neighbor

    embedding. (2012)

  • Huang, J.B., Singh, A., Ahuja, N.: Single image super-resolution

    from transformed self-exemplars. In: Computer Vision and Pattern

    Recognition (CVPR), 2015 IEEE Conference on, IEEE (2015) 5197–

    5206

6、指标：

  • RMSE（Root Mean Squared Error）
  • SSIM（Structure Similarity of Index）
  • MAE（Mean Absolute Error）

7、分析：

  • The complexity of the non-linear mapping depends on the up-sampling factor

  • 1st训练阶段的结果存在环形伪影ring-effect

    截屏2025-10-29 15.50.50

8、改进：

Image Super-Resolution Using Deep Convolutional Networks

1、研究目标：

2、难点：

3、背景：

4、方法：

超分辨卷积神经网络

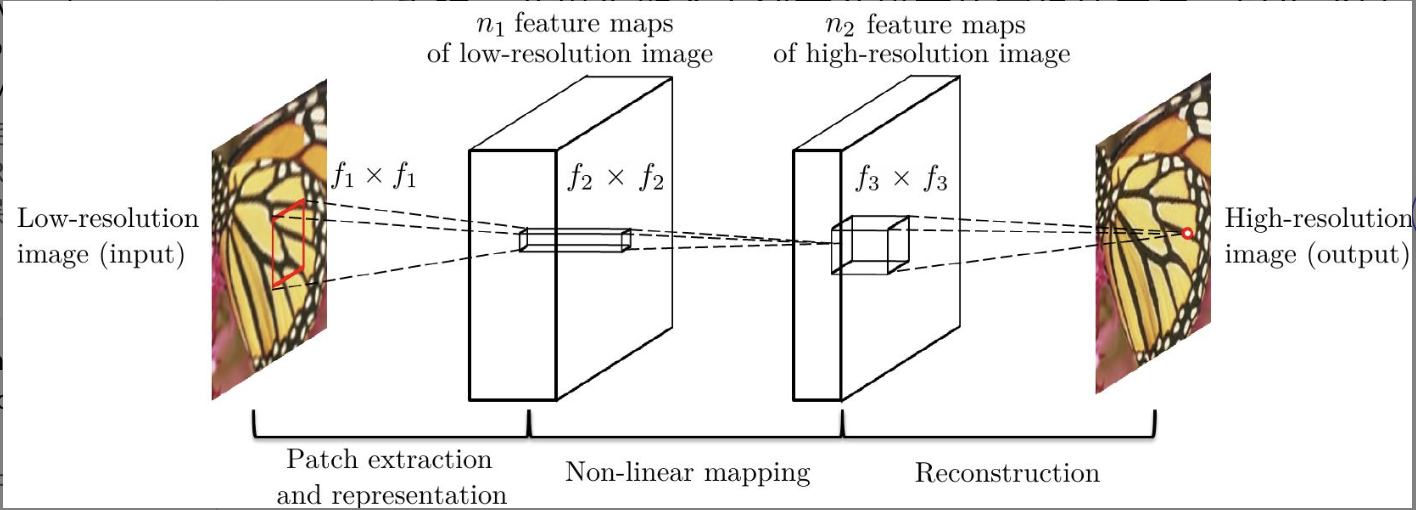
  1. 输入低分辩率深图经双向三次插值到高分辨率作为整个网络的初始输入Y（和高分辨图像的尺寸一致），经过网络后的图像F(Y), 实际的高分辨图像X。

  2. 网络F包括三部分：

    • 块的提取和表示：从Y图提取若干区块（可重叠），将每一个区块表示为高维特征向量，若干特征向量构成一组特征图，而且特征图的数量由特征向量的维度决定。该层网络表示为$F_1(Y)=\max(0,W_1Y+B_1)=\hat{Y}$, $W_1$对应着$n_1$个卷积核$(c,f_1,f_1)$,卷积核数量$n_1$即输出的特征数, 输入的特征数量$c$, 核的尺寸$f_1$。$B_1$对应着$n_1$个和卷积核关联的偏移量。激活函数使用ReLU，max(0, x)作用于卷积输出量$W_1Y+B_1$。

    • 非线性映射：将每个高维向量映射为另一个高维向量，但是此高维向量是高分辨率图像中某个块的高维向量表示。$$F_2(\hat{Y})=\max(0,W_2*\hat{Y}+B_2)=\tilde{Y}$$使用$n_2$个卷积核$(n_1,1,1)$计算$F_1$的输出特征，这里使用$1\times1$的核是对原始图的每一个区块做非线性映射，如果推广为$3\times3$等，表示对原始图的$3\times3$个区块共同做非线性映射，映射成一个高维向量。

    • 重构：汇集所有高分辨率区块的向量表示生成高分辨率图像，并期望重构图和真实图相似。在传统方法中，通常将预测的重叠高分辨率图像块进行平均，以生成最终的完整图像。依然使用卷积层重构图像$$F_3(\tilde{Y})=W_3*\tilde{Y}+B_3=\bar{Y}$$, $W_3$对应着$c$个卷积核$(n_2,f_3,f_3)$。$W_3$起到两个作用（1）将特征空间的系数表示的特征转会图像空间表示，（2）各图像块之间的重叠区域的加权平均。

    • 三种操作都是卷积层形式但是背后的动机不同。

    image-20251028133945621

训练

网络参数$\Theta={W_1,W_2,W_3,B_1,B_2,B_3}$,重构图$F(Y;\Theta)$,一组真实的高分辨图${X_i}$以及对应的低分辩图${Y_i}$, 损失函数使用均方误差MSE。

$$L(\Theta) = \frac{1}{n}\sum_{i=1}^n||$F(Y_i;\Theta)-X_i||^2$$

5、相关研究：

6、指标：

7、分析：

8、改进：

Fast and accurate image upscaling with super-resolution forests

github

1、研究目标：

2、难点：

3、背景：

4、方法：

设有N个低分辩图像样本构成低分辩图像域$X_L\in\mathbb{R}^{D_L\times N}$，同样高分辨率图像域为$X_H\in\mathbb{R}^{D_H\times N}$，其中一个样本分别表示为$\mathbf{x}_L\in\mathbb{R}^{D_L}$和$\bold{x}_H\in\mathbb{R}^{D_H}$。

学习从低分辨率图像域到高分辨图像域的映射问题可由公式$\hat{\bold{x}}_H = W(\bold{x}_L)\cdot\bold{x}_L$表示，映射W的构建依赖数据$\bold{x}_L$。

随机森林实现映射细节

  • 平方损失函数的优化参数的过程：$\mathop{\arg\min}\limits_{W(\bold{x}L)}\sum{n=1}^N||\bold{x}_H^n-W(\bold{x}_L^n)\cdot\bold{x}_L^n||^2$

  • 对$\bold{x}_L^n$用函数$\phi$构造若干新的特征$\phi_j(\bold{x}_L^n);j=1,2,\cdots,\gamma+1$​

​ $\mathop{\arg\min}\limits_{W(\bold{x}L),\forall j}\sum{n=1}^N||\bold{x}_H^n-W_j(\bold{x}_L^n)\cdot\phi_j(\bold{x}_L^n)||^2$

  • 随机森里由T个树构成$\mathcal{T}_t(x):\mathcal{X}\rightarrow\mathcal{Y}, , t=1,2,\cdots,T$，这里$\mathcal{X}\in\mathbb{R}^{D}$是输入特征空间，$\mathcal{Y}$是输出的标签空间。根据任务标签空间表示不同，例如分类任务$\mathcal{Y}={1,2,\cdots,C}$， C是标签数目；在多变量回归任务中$\mathcal{Y}=\mathbb{R}^{D_H}, \mathcal{X}=\mathbb{R}^{D_L}$，高分辨图像的特征数为$D_H$，低分辨图像的特征数为$D_L$。

  • 每棵树$\mathcal{T}_t$将数据空间$X_L\in\mathbb{R}^{D_L\times N}$划分到L个不连接的叶子节点$l=1,2,\cdots,L$上处理。在每个也叶子节点上学习一个线性模型$m_l(\bold{x}L)=\sum{j=0}^\gamma W^l_j\cdot\phi_j(\bold{x}_L)$​。

  • 整合所有树的预测结果并做平均化处理就得到数据依赖的映射$W(\bold{x}_L)$。

    $\hat{\bold{x}}_H=m(\bold{x}_L)=W(\bold{x}L)\cdot\bold{x}L=\frac{1}{T}\sum{t=1}^Tm{l(t)}(\bold{x}_L)$​

    $l(t)$是样本$\bold{x}_l$被路由到第t棵树的叶子节点，$m(\bold{x}_L)$是多棵树在$l$节点上的综合预测线性模型。

数据样本$\bold{x}_L$​的路由规则：

  • 用发现分割函数循环化分练数据集$X_H$中的样本到不同的节点子集中。划分始于树的根节点一直向树的下部路由直到达到最深处$\xi_{max}$并创建叶子节点。

    $\sigma(\bold{x}L,\Theta)=\begin{cases}0\quad \mathrm{if}; r\Theta(\bold{x}_L)\lt0\ 1\quad\mathrm{otherwise}\end{cases}$​

    $\Theta$定义了响应函数

    • $r_\Theta(\bold{x}L)=\bold{x}L[\Theta_1]-\Theta{th}$，这里的算子$[\cdot]$索引样本$\bold{x}L$的某个维度，$\Theta*\in{1,2,\cdots,D_L}\subset\mathbb{Z}$，$\Theta{th}\in\mathbb{R}$​ 是阈值。
    • $r_\Theta(\bold{x}_L)=\bold{x}_L[\Theta_1]-\bold{x}L[\Theta_2]-\Theta{th}$​​
    • 从${1,2,\cdots,D_L}$中随机采样一组数作为参数值$\Theta$

  • 由$\Theta$决定的分割函数$\sigma(\bold{x}_L,\Theta)$划分数据集的质量评价公式为

    $Q(\sigma,\Theta,X_H,X_L)=\sum\limits_{c\in{Le,Ri}}|X^c|\cdot E(X^c_H,X_L^c)$​

    这里的$Le$和$Ri$定义了左节点和右节点，$|\cdot|$是取模，$|X|$即路由到节点上的样本数量，$X^{Le}{\textbraceleft H,L\textbraceright}={\bold{x}{\textbraceleft H,L\textbraceright}:\sigma(\bold{x}L,\Theta)=0},X^{Re}{H,L}={\bold{x}_{\textbraceleft H,L\textbraceright}:\sigma(\bold{x}_L,\Theta)=1}$，$E(X_H,X_L)$测量数据集间的致密性或纯度，即相似的数据落入到相同的节点中处理。

    • $E(X_H,X_L)=\frac{1}{X}\sum\limits_{n=1}^{|X|}(||\bold{x}_H^n-m(\bold{x}_L^n)||^2_2+\kappa\cdot||\bold{x}_L^n-\bar{\bold{x}}_L||^2_2)$​

      $\bar{\bold{x}}_L$是$\bold{x}_L^n$的平局值，$\kappa$视作超参。

5、相关研究：

6、指标：

7、分析：

8、改进:

Bayesian Image Super-Resolution With Deep Modeling of Image Statistics

github

1、研究目标：

2、难点：

3、背景：

4、方法：

Notion Symbol
Scalar
Vector
Matrix		 lowercase letter, e.g., $a$
boldface lowercase letter, e.g., $\bold{a}$
boldface capital letter, e.g., $\bold{A}$
Observation/Reference
Restoration
Smoothness component
Sparsity residual
Gaussian noise
Deterministic downsampling matrix
Identity matrix		 $\bold{y}\in\mathbb{R}^{d_y}/\bold{u}^*\in\mathbb{R}^{d_u}$
$\bold{u}\in\mathbb{R}^{d_u}$
$\bold{x}\in\mathbb{R}^{d_u}$
$\bold{z}\in\mathbb{R}^{d_u}$
$\bold{n}\in\mathbb{R}^{d_y}$
$\bold{A}\in\mathbb{R}^{d_y\times d_u}$
$\bold{I}$
Spatial correlation w.r.t. $\bold{x}$
Sparsity precision w.r.t. $\bold{z}$
Noise mean/strength w.r.t. $\bold{n}$		 $\boldsymbol{\upsilon}\in\mathbb{R}^{d_u}$
$\boldsymbol{\omega}\in\mathbb{R}^{d_u}$
$\bold{m}\in\mathbb{R}^{d_y}$/$\boldsymbol{\rho}\in\mathbb{R}^{d_y}$
Mean/Deviation of VDs
Normal/Gamma distribution
Hyperparameters(下采样，卷积核，高斯先验均值，高斯先验方差，伽马先验形状参数，伽马先验比例参数，)		 $\breve{\bold{u}\cdot}/\breve{\bold{\sigma}\cdot}$
$\mathcal{N}(\cdot,\cdot)/\mathcal{G}(\cdot,\cdot)$
$s, \bold{k}\in\mathbb{R}^{d_k}, \boldsymbol{\mu}_0, \sigma_0, \boldsymbol{\phi}, \boldsymbol{\gamma}, \lambda, \tau$
$\ell_1/\ell_2/\bold{M}$ norm
inner-product		 $\lVert\cdot\rVert_1/\lVert\cdot\rVert_2/\lVert\cdot\rVert_\bold{M}$
$<\cdot,\cdot>$

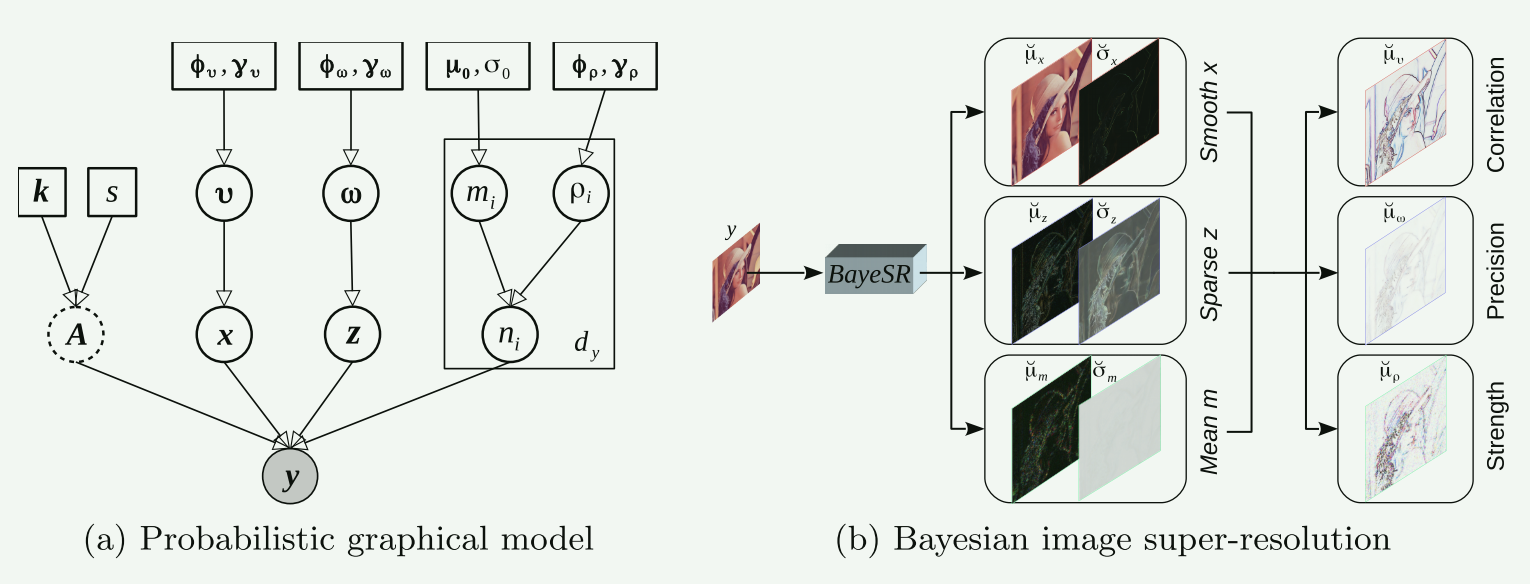
image-20251120162153286

  • 低分辨率图使用图像平滑成分+零星的图像高频残差实现超分辨图像。

  • 低分辨率图像作为观测图像$\bold{y}$，高分辨图像作为参考图像$\bold{u}^*$，则图像的退化表达式：

    $\bold{y}=\bold{A}(\bold{x}+\bold{z})+\bold{n}$​

    图像平滑成分$\bold{x}$, 图像稀疏残差$\bold{z}$, 图像高斯噪声$\bold{n}$, 下采样矩阵$A$, $\bold{A}\bold{x}$可以通过卷积和下采样实现。

构建先验分布

  • $\bold{y}$的似然函数

    $p(\bold{y}|\bold{A},\bold{x},\bold{z},\bold{m},\boldsymbol{\rho})=\mathcal{N}(\bold{y}|\bold{A}(\bold{x}+\bold{z})+\bold{m},\mathrm{diag}(\boldsymbol{\rho})^{-1})$

  • 噪声$\bold{n}$建模为高斯噪声均值为$\bold{m}$，方差$\mathrm{diag}(\boldsymbol{\rho})^{-1}\in\mathbb{R}^{d_y\times d_y}$​

    $p(\bold{n}|\bold{m},\boldsymbol{\rho})=\mathcal{N}(\bold{n}|\bold{m}, \mathrm{diag(\boldsymbol{\rho})^{-1}})$​

    • 噪声均值$\bold{m}$​先验分布服从高斯分布。

      $p(\bold{m}|\boldsymbol{\mu}_0,\sigma_0)=\mathcal{N}(\bold{m}|\boldsymbol{\mu}_0,(\sigma_0\bold{I})^{-1})$

    • 噪声强度$\boldsymbol{\rho}$​先验分布服从Gamma分布。

      $p(\boldsymbol{\rho}|\boldsymbol{\phi}\rho,\boldsymbol{\gamma}\rho)=\prod\limits_{i=1}^{d_y}\mathcal{G}(\rho_i|\phi_{\rho i},\gamma_{\rho i})$​

  • 分段平滑图像$\bold{x}$的先验分布

    $p(\bold{x}|\boldsymbol{\upsilon})=\mathcal{N}(\bold{x}|\bold{0},[\bold{D}_h^T\mathrm{diag(\boldsymbol{\upsilon})}\bold{D}_h + \bold{D}_v^T\mathrm{diag(\boldsymbol{\upsilon})}\bold{D}_v])^{-1}$

    • 此分布依据马尔可夫随机场，像素之间的相关性由二次能量函数定义$E(\bold{x})=\frac12\bold{x}^T\bold{Q}\bold{x}$。随机变量$\bold{x}$的能量分布服从指数分布$p(x)\propto\exp(-E(\bold{x}))$，而$\bold{x}$服从高斯分布$\mathcal{N}(\bold{x}|\bold{0},\bold{Q}^{-1})$。

    • 总变差用于图像正则化，最小化梯度范数，常用的平滑性惩罚项是梯度的 $L_2$ 范数平方，即： $\left|\mathbf{D}{h} \mathbf{x}\right|^{2}+\left|\mathbf{D}{v} \mathbf{x}\right|^{2}=\bold{x}^T\bold{D}_h^T\bold{D}_h\bold{x}+\bold{x}^T\bold{D}_v^T\bold{D}_v\bold{x}=\bold{x}^T(\bold{D}_h^T\bold{D}_h+\bold{D}_v^T\bold{D}_v)\bold{x}$

    • 图像$\bold{x}$空间相关性强度用$\boldsymbol{\upsilon}$​表示，相当于空间权重，越大图像在该区域越平滑。

    空间相关性强度$\boldsymbol{\upsilon}$服从Gamma先验。

    $p(\upsilon|\boldsymbol{\phi}v, \boldsymbol{\gamma}v)=\prod\limits{i=1}^{d_y}\mathcal{G}(\upsilon_i|\phi{\upsilon i},\gamma_{\upsilon i})$​​

  • 稀疏残差图像$\bold{z}$​服从学生先验分布，使用边缘化三参数正态-伽马分布。

    $\begin{align*}p(\bold{z}|\boldsymbol{\phi}\omega,\boldsymbol{\gamma}\omega) &= \int_{\mathbb{R}^{d_u}}p(\bold{z}|\boldsymbol{\omega})p(\boldsymbol{\phi}\omega,\boldsymbol{\gamma}\omega)d\boldsymbol{\omega}\ &= \prod\limits_{i=1}^{d_u}\int_\mathbb{R}\mathcal{N}(z_i|0,\omega_i^{-1})\mathcal{G}(\omega_i|\phi_{\omega i},\gamma_{\omega i})d\omega_i\end{align*}$​

    $p(\boldsymbol{\omega}|\boldsymbol{\phi}\omega,\boldsymbol{\gamma}\omega)=\prod\limits_{i=1}^{d_u}\mathcal{G}(\omega_i|\phi_{\omega i},\gamma_{\omega i})$

通过变分贝叶斯推断来估计给定y时这些变量的后验分布

  • 待求后验估计参量集$\psi={\bold{m},\boldsymbol{\rho},\bold{x},\boldsymbol{\upsilon},\bold{z},\boldsymbol{\omega}}$​。

  • 贝叶斯计算后验分布(似然*先验)：

    $p(\psi|\bold{y})\propto p(\bold{y}|\psi)p(\psi)$​

    变分贝叶斯后验分布：

    $q(\psi)=q(\bold{m})q(\boldsymbol{\rho})\prod\limits_{i=1}^{d_u}q(x_i)q(\boldsymbol{\upsilon})\prod\limits_{i=1}^{d_u}q(z_i)q(\boldsymbol{\omega})$​

  • 最小化变分贝叶斯后验分布和贝叶斯后验分布的KL散度，获取待估计参量的变分后验分布

    $\begin{align*}&\breve{q}(\psi)\in\mathop{\arg\min}\limits_{q(\psi)}\ KL(q(\psi)||p(\psi|\bold{y}))\ &\Leftrightarrow\ &\min\limits_{\breve{q}(\psi)}KL(\breve{q}(\psi)\lvert\rvert p(\psi))-\mathbb{E}_{\breve{q}(\boldsymbol{\rho})}[\log p(\bold{y}|\psi)]\end{align*}$

    $\begin{align*}\breve{q}(\bold{m})&=\mathcal{N}(\bold{m}|\breve{\boldsymbol{\mu}}m,\mathrm{diag}(\breve{\boldsymbol{\sigma}}m^2)),\ \breve{q}(\boldsymbol{\rho})&=\prod\limits{i=1}^{d_y}\mathcal{G}(\rho_i|\breve{\beta}{\rho i},\breve{\alpha}{\rho i}),\ \breve{q}(\bold{x})&=\mathcal{N}(\bold{x}|\breve{\boldsymbol{\mu}}x,\mathrm{diag}(\breve{\boldsymbol{\sigma}}x^2)),\ \breve{q}(\boldsymbol{\upsilon})&=\prod\limits{i=1}^{d_y}\mathcal{G}(\upsilon_i|\breve{\beta}{\upsilon i},\breve{\alpha}{\upsilon i}),\ \breve{q}(\bold{z})&=\mathcal{N}(\bold{z}|\breve{\boldsymbol{\mu}}z,\mathrm{diag}(\breve{\boldsymbol{\sigma}}z^2)),\ \breve{q}(\boldsymbol{\omega})&=\prod\limits{i=1}^{d_y}\mathcal{G}(\omega_i|\breve{\beta}{\omega i},\breve{\alpha}_{\omega i})\end{align*}$​

优化目标

  • 后验变量损失$\mathcal{L}_{var}$
    • $\mathcal{L}_y$: 恢复的高分辨图像与真实图像的损失。
    • $\mathcal{L}_{\breve{\mu}_x}$: 逐段平滑图像产生的损失。
    • $\mathcal{L}_{\breve{\sigma}_x}$: 逐段平滑图像偏离均值为1的分布的损失。
    • $\mathcal{L}_{\breve{\mu}_z}$: 稀疏高频图像产生的损失。
    • $\mathcal{L}_{\breve{\sigma}_z}$: 稀疏高频图像偏离均值为1的分布的损失。
    • $\mathcal{L}_{\breve{\mu}_m}$: 噪声图像产生的损失。
    • $\mathcal{L}_{\breve{\sigma}_m}$: 噪声图像偏离均值为1的分布的损失。

参数的后验分布由神经网络给出

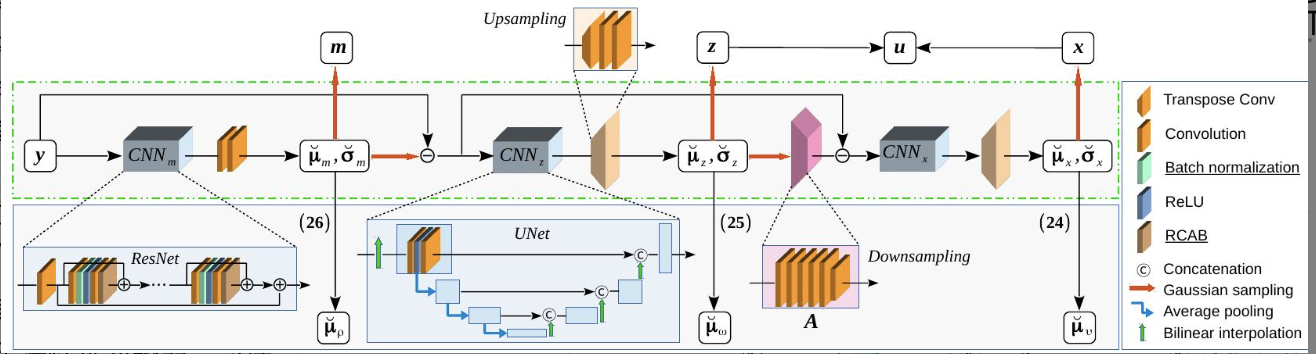
image-20251121164615935

  1. 构建三个模块，以连续推断关于噪声均值m、稀疏残差z和平滑分量x的变分参数。
  2. 计算关于空间相关性υ、稀疏精度ω和噪声强度ρ的变分参数。
  3. 随机样本u = x + z被认为是y的重建。
  4. $\boldsymbol{\mu},\boldsymbol{\sigma}$参数的后验分布是神经网络中的特征图，由神经网络参数$\boldsymbol{\theta_G}$决定。

  • 初始阶段，先预训练下采样卷积网路$\boldsymbol{A}$。已知高分辨图像$\bold{u}_i^*$和低分辨图像$\bold{y}_i$通过MSE指标训练。学习完后后序阶段网络参数冻结。

  • 非监督训练阶段，借助生成学习、判别式学习和生成对抗学习训练贝叶斯神经网络。

    • 生成学习的优化损失是变量损失$\mathcal{L}_{var}(\boldsymbol{\theta}_G)$​

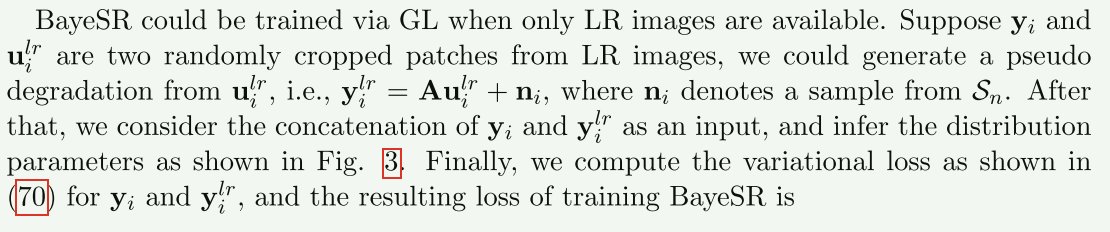
      image-20251125210911380

      $\mathcal{L}{var}(\boldsymbol{\theta}G)=\frac1N\sum\limits{i=1}^N[\mathcal{L}{var}(\bold{y}i+\mathcal{L}{var}(\bold{y}_i^{lr})]$

    • 判别式学习的优化损失是自监督损失$\mathcal{L}_{self}(\boldsymbol{\theta}_G)$​​​

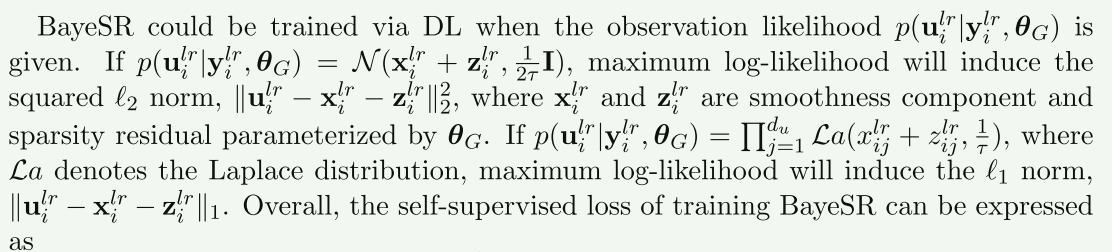
      image-20251125211311542

      $\mathcal{L}_{self}(\boldsymbol{\theta}G)=\frac1N\sum\limits{i=1}^N\lVert\bold{u}_i^{lr}-\bold{x}_i^{lr}-\bold{z}_i^{lr}\rVert^p_p$​

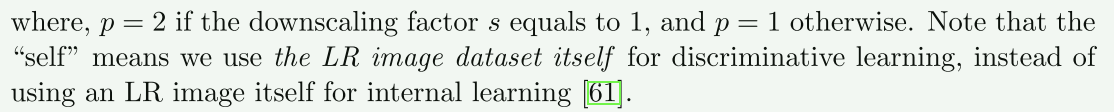
      image-20251125211333890

    • 生成对抗学习的优化损失是生成损失$\mathcal{L}_{gen}(\boldsymbol{\theta}_G)$​​​

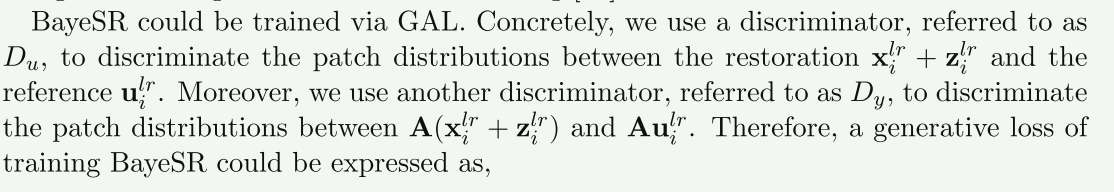
      image-20251125211652945

      $\mathcal{L}_{gen}(\boldsymbol{\theta}G)=\frac1N\sum\limits{i=1}^N\log[1-D_u(\bold{x}_i^{lr}+\bold{z}i^{lr})]+\frac1N\sum\limits{i=1}^N\log[1-D_y(\bold{A}(\bold{x}_i^{lr}+\bold{z}_i^{lr}))]$

    • 总体优化

      $\min\limits_{\boldsymbol{\theta}G}\mathcal{L}{var}(\boldsymbol{\theta}G)+\mathcal{L}{self}(\boldsymbol{\theta}G)+\mathcal{L}{gen}(\boldsymbol{\theta}_G)$

5、相关研究：

6、指标：

7、分析：

8、改进：

SwinIR: Image Restoration Using Swin Transformer

[github](SwinIR: Image Restoration Using Swin Transformer)

1、研究目标：

In this paper, we propose a strong baseline model SwinIR for image restoration based on the Swin Transformer

2、难点：

3、背景：

4、方法：

SwinIR consists of three parts: shallow feature extraction, deep feature extraction and high-quality image reconstruction。

不同的任务（超分辨、去噪、图像压缩）使用相同的特征提取模块但是使用不同的重构模块。

浅层和深层特征提取

  • 低质量图片$I_{LQ}\in\mathbb{R}^{H\times W\times C_{in}}$, 使用3x3卷积层$H_{SF}(\cdot)$提取浅层特征$F_0\in\mathbb{R}^{H\times W\times C}$​, 一般为低频特征

    $F_0 = H_{SF}(I_{LQ})$​​

  • 使用深度特征提取模块$H_{DF}(\cdot)$从$F_0$中提取深层特征$F_{DF}\in\mathbb{R}^{H\times W\times C}$​，一般为高频特征

    $F_{DF} = H_{DF}(F_0)$​

    • $H_{DF}$​包含K个残差Swin Transformer计算块（RSTB）和一个3x3 卷积层。

    • 每一个RSTB计算块都会产生一个中间特征$F_i, i=1,\cdots, K$

      • $F_i=H_{RSTB_i}(F_{i-1}), i=1,\cdots, K$​​

        • 一个$RSTB_i$​模块有L层Swin Transformer

          $F_{i,j}=H_{STL_{i,j}}(F_{i,j-1}), j=1,\cdots,L$​

          • Swin Transformer由transformer模块（由层归一化、多头注意力残差、多层感知计算构成）和移动窗（局部注意力）构成。
            1. 输入的数据形状为$H\times W\times C$​
            2. 变形：$\frac{HW}{M^2}\times M^2\times C$， 将输入量分成相互不重叠的$M\times M$大小的局部窗口。
            3. 每个窗口中进行自注意力计算

        • 一个$RSTB_i$模块的最后一层使用卷积以及一个残差计算

          $F_{i,out}=H_{Conv_i}(F_{i,L})+F_{i,0}$

      • $F_{DF} = H_{Conv}(F_K)$​

图像重构

  • 浅层和深层特征融合后重构高质量图像

    $I_{RHQ}=H_{REC}(F_0+F_{DF})$​

损失函数

轻量图片可以用$L_1$范数损失

$\mathcal{L}=\lVert I_{RHQ}-I_{HQ}\rVert_1$​​

生活图片可以使用生成对抗损失，百分比损失。

图像压缩、去噪可以使用Charbonnier损失

$\mathcal{L}=\sqrt{\lVert I_{RHQ}-I_{HQ}\rVert^2+\epsilon^2}$

5、相关研究：

The convolution layer is good at early visual processing, leading to more stable optimization and better results [^SwinIR_1]

[^SwinIR_1]: Tete Xiao, Mannat Singh, Eric Mintun, Trevor Darrell, Piotr Doll´ar, and Ross Girshick. Early convolutions help
transformers see better. arXiv preprint arXiv:2106.14881, 2021. 2
6、指标：

7、分析：

8、改进：

Pulling Things out of Perspective

1、目标：

当前最先进的单视图深度估计和语义分割方法的局限性与透视几何的性质密切相关，即物体的感知大小与距离成反比。利用此性质简化像素级深度分类器为只预测像素在任意规范深度位置处的可能性。

7、分析：

掩码图像编码--------------------------------------------------------------------

Masked Autoencoders Are Scalable Vision Learners

GitHub

1、研究目标：

自编码最早用于NLP，自编码在语言和视觉上的差异是什么？

2、难点：

  • Q：图像处理大多用卷积，卷积作用在规则网格上，无法集成作为指示器的掩码词牌以及位置嵌入向量。

    A: Vision Transformers (ViT)，图像分块，像处理自然语言一样处理图像块序列。每个图像块展平为向量用线性投影映射到固定维度的嵌入空间中形成一个token。线性投影相当于1x1卷积。

  • 图像和语言的信息密度不同，语言的信息密度大，因此句子中部分单词的缺失会让模型挖掘和理解深层次的语意。图像具有空间冗余性（空间相邻的像素存在高度相关性和相似性），因此图像中缺失一块图元模型更会通过挖掘低层次信息（纹理、颜色）恢复图像，缺少对高层图像理解（场景、对像）。

    A：在图像中随机屏蔽遮挡大量图像块，破坏掉图像的冗余信息。创造了自监督学习任务。

  • Q: 在自编码的解码器中，它会将潜藏表示映射回图像，但是相比图像的识别任务重构的像素具有更多的低级语意。

    A：使用掩码自编码，非对称设计编码和解码，编码器只对可见图像块编码，而解码器根据潜藏表示和掩码词牌重构图像。

3、背景：

4、方法：

  • 非对称编解码架构，编码部分只对可见图像块操作；解码部分从潜藏表示和掩码词牌中重构图像。
  • 使掩码比重达到75%以上可以产生自监督学习。

5、相关研究：

  • 掩码语言模型
  • 自编码
  • 屏蔽图像编码
  • 自监督学习

6、指标：

7、分析：

8、改进：

时间序列-------------------------------------

SimVP: Simpler yet Better Video Prediction

GitHub

1、研究目标：

提供一种更简单的只用CNN网络预测视频。

2、难点：

  • 视频具有复杂性和随机性。
  • 不同模型使用不同的指标和数据，缺少对好性能必要性的理解。
  • 不同的代码框架、各自的独特技巧很难公平对比。

3、背景：

  • Vedio prediction, climate change, human motion, traffic flow.
  • RNN架构，transformer架构，自回归、归一化流，针对训练策略的对抗神经网络训练。
  • 视频预测模型分4类：
    • RNN模块堆叠
    • CNN-RNN-CNN堆叠
    • CNN-ViT-CNN堆叠
    • CNN-CNN-CNN堆叠

4、方法：

  • 问题描述：

一个在$t$时刻包含了过去$T$个帧的视频序列$X_{t,T}={x_i}^t_{t-T+1}, i=t-T+1,\cdots, t$，需要预测$t$时刻未来$T^\prime$个帧的视频序列$Y_{t,T^\prime}={x_i}^{t+T^\prime}{t+1}$，其中第$i$帧的图片$x_i\in\mathbb{R}^{C,H,W}$具有通道数C, 图像尺寸HxW。预测模型为$\mathcal{F}\Theta: X_{t,T}\mapsto Y_{t,T^\prime}$，待学习和优化的参数为$\Theta$，通过损失函数$\mathcal{L}$优化参数为$\Theta^* = \arg,\min\limits_\Theta\mathcal{L}(\mathcal{F}\Theta(X{t,T}),Y_{t,T^\prime})$，损失函数可以任意选取，这里使用MSE损失函数。

  • 架构

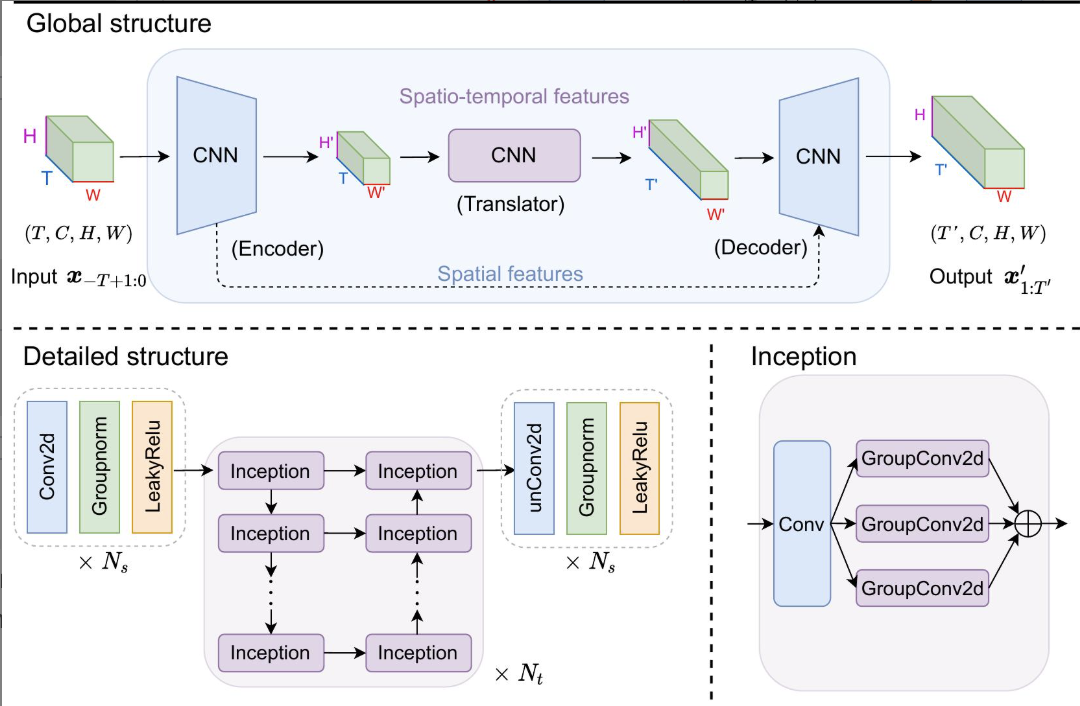
image-20251030111016684

SimVP架构包含：

  • 编码器（CNN构成）：提取空间特征。
  • 转换器（CNN构成）：学习时间演化。
  • 解码器（CNN构成）：汇总时空信息预测未来帧。

编码器

堆砌$N_s$ 个ConvNormReLU（Conv2d+LayerNorm+LeakyReLU） 模块, $z_i=\sigma(LayerNorm(Conv2d(z_{i-1}))), 1\le i \le N_s$， 输入和输出$z_{i-1}, z_{i}$的形状分别为 $(T, C,H,W)$和$(T, \hat{C},\hat{H},\hat{W})$​

转换器

使用$N_t$个Inception模块在$(H,W)$图像对$T\times C$​个通道（时空特征）进行卷积。Inception中Conv核是1x1，并列的三个GroupConv2d的卷积核分别是1x1, 3x3, 5x5。

$$z_j=Inception(z_{j-1}), N_s<j\le N_s+N_t$$

输入$z_{j-1}$, 输出$z_j$的形状分别为$(T\times C,H,W)$和$(\hat{T}\times\hat{C},H,W)$​

解码器

使用$N_s$个unConvNormReLU（ConvTranspose2d+GroupNorm+LeakyReLU）模块重构出预测帧，在$(H,W)$的图像上对$C$ 个通道进行卷积。

$z_i=\sigma(GroupNorm(unConv2d(z_{i-1}))), N_s+N_t\le i \le 2N_s+N_t$

输入$z_{j-1}$, 输出$z_j$的形状分别为$(\hat{T},\hat{C},H,W)$和$(T, C,H,W)$​， 反卷积操作使用ConvTranspose2d。

优化

$\min\limits_\Theta\mathcal{L}(\mathcal{F}\Theta(X{t,T}),Y_{t,T^\prime})$​

实验方案

数据只选择共用的数据集, 指标上如果原文中提供就首选原文指标，忽略复现方法的差异性。

5、相关研究：

  • SHI Xingjian, Zhourong Chen, Hao Wang, Dit-Yan Yeung, Wai-Kin Wong, and Wang-chun Woo. Convolutional lstm network: A machine learning approach for precipitation nowcasting. In Advances in neural information processing systems, pages 802–810, 2015. 1, 2, 5, 6, 7
  • Yunbo Wang, Mingsheng Long, Jianmin Wang, Zhifeng Gao, and Philip S Yu. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the 31st International Conference on Neural Information Processing Systems, pages 879–888, 2017. 1, 2, 5, 6, 7
  • Marc Oliu, Javier Selva, and Sergio Escalera. Folded recurrent neural networks for future video prediction. In Proceedings of the European Conference on Computer Vision (ECCV), pages 716–731, 2018. 2, 7
  • Yunbo Wang, Lu Jiang, Ming-Hsuan Yang, Li-Jia Li, Mingsheng Long, and Li Fei-Fei. Eidetic 3d lstm: A model for video prediction and beyond. In International conference on learning representations, 2018. 1, 2, 5, 6, 7, 12
  • Vincent Le Guen and Nicolas Thome. Disentangling physical dynamics from unknown factors for unsupervised video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11474– 11484, 2020. 1, 2, 4, 5, 6, 12
  • Dirk Weissenborn, Oscar Tackstr¨ om,¨ and Jakob Uszkoreit. Scaling autoregressive video models. arXiv preprint arXiv:1906.02634, 2019. 1, 2, 3, 5
  • Ruslan Rakhimov, Denis Volkhonskiy, Alexey Artemov, Denis Zorin, and Evgeny Burnaev. Latent video transformer. arXiv preprint arXiv:2006.10704, 2020. 1, 2, 3, 5
  • Hang Gao, Huazhe Xu, Qi-Zhi Cai, Ruth Wang, Fisher Yu, and Trevor Darrell. Disentangling propagation and generation for video prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 9006– 9015, 2019. 2, 3, 7
  • Yong-Hoon Kwon and Min-Gyu Park. Predicting future frames using retrospective cycle gan. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1811–1820, 2019. 2, 7
  • Viorica Patraucean, Ankur Handa, and Roberto Cipolla. Spatio-temporal video autoencoder with differentiable memory. arXiv preprint arXiv:1511.06309, 2015. 2
  • Lluis Castrejon, Nicolas Ballas, and Aaron Courville. Improved conditional vrnns for video prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 7608–7617, 2019. 2
  • Hugo Touvron, Matthieu Cord, Matthijs Douze, Francisco Massa, Alexandre Sablayrolles, and Herve´ Jegou. ´ Training data-efficient image transformers & distillation through attention. In International Conference on Machine Learning, pages 10347–10357. PMLR, 2021. 2
  • Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, and Baining Guo. Swin transformer: Hierarchical vision transformer using shifted windows. arXiv preprint arXiv:2103.14030, 2021. 2
  • Daniel Neimark, Omri Bar, Maya Zohar, and Dotan Asselmann. Video transformer network. arXiv preprint arXiv:2102.00719, 2021. 2
  • Anurag Arnab, Mostafa Dehghani, Georg Heigold, Chen Sun, Mario Luciˇ c,´ and Cordelia Schmid. Vivit: A video vision transformer. arXiv preprint arXiv:2103.15691, 2021. 2
  • Gedas Bertasius, Heng Wang, and Lorenzo Torresani. Is space-time attention all you need for video understanding? arXiv preprint arXiv:2102.05095, 2021. 2
  • Haoqi Fan, Bo Xiong, Karttikeya Mangalam, Yanghao Li, Zhicheng Yan, Jitendra Malik, and Christoph Feichtenhofer. Multiscale vision transformers. arXiv preprint arXiv:2104.11227, 2021. 2
  • Ze Liu, Jia Ning, Yue Cao, Yixuan Wei, Zheng Zhang, Stephen Lin, and Han Hu. Video swin transformer. arXiv preprint arXiv:2106.13230, 2021. 3, 5
  • Ziwei Liu, Raymond A Yeh, Xiaoou Tang, Yiming Liu, and Aseem Agarwala. Video frame synthesis using deep voxel flow. In Proceedings of the IEEE International Conference on Computer Vision, pages 4463–4471, 2017. 2, 3, 6, 7
  • Ziru Xu, Yunbo Wang, Mingsheng Long, Jianmin Wang, and MOE KLiss. Predcnn: Predictive learning with cascade convolutions. In IJCAI, pages 2940–2947, 2018. 2, 3
  • Hsu-kuang Chiu, Ehsan Adeli, and Juan Carlos Niebles. Segmenting the future. IEEE Robotics and Automation Letters, 5(3):4202–4209, 2020. 2, 3
  • Osamu Shouno. Photo-realistic video prediction on natural videos of largely changing frames. arXiv preprint arXiv:2003.08635, 2020. 2, 3, 7

6、指标：

  • MSE、MAE、SSIM、PSNR
  • 每个训练周期的运行时间
  • 每个样本在显存中占用
  • 单张图片的每秒浮点数运算FLOPS (floating point operations per second)，即吞吐量，越高计算越快

​ 区分FLOPs (Floating Point Operations), 指运算量，越低越好。

7、分析：

  • SimVP is much simpler than PhyDNet and CrevNet, without using RNN, LSTM, or complicated modules, which are considered as the important reason for performance improvement.
  • it is promising to achieve better performance with a extremely simple model. Perhaps previous works pay too much attention to the model complexity and novelty, and it’s time to go back to basics because a simpler model makes things clearer.
  • Simplicity leads to efficiency，简单高效意味着更易扩展和使用
  • 自己框架的转换器组件由CNN, RNN和T transformer的模块替换对比，展示哪种模块有利于视频预测。
  • we may modify a few implementation details without changing the core algorithm。
  • 训练稳定后RNN比CNN的损失值更容易受大的学习率影响。
  • 基于CNN的方法的一个可能的局限性是，它可能难以扩展到具有灵活长度的预测
  • Q: 在其他数据集中能否SOTA？途径：扩展数据集。A:yes.
  • Q: 在其他数据集中是否具有良好泛化能力？途径：用一个新的样本集直接测试。A:yes.
  • Q：能否扩展到灵活预测长度？途径：基于CNN的方法的一个可能的局限性是，它可能难以扩展到具有灵活长度的预测。通过模仿RNN的迭代过程来处理,即最近的预测结果作为输入。A:yes.
  • Q: 架构中哪一部分对性能的提升起到关键作用？途径：消融，控制训练周期100，改变模块的参数指标，替换模块，去掉模块等。
  • Q: 卷积核如何影响性能？途径：消融
  • Q：编码、转换、解码分别扮演什么角色？途径：消融，首先三部分训练n个周期，三部分的保存参数$E_n, T_n, D_n$, 然后再训练m个周期，三部分的保存参数$E_m, T_m, D_m$, 控制任意两个部分用相同的周期参数，对比剩余部分的不同周期的参数在模型最后一层预测的结果。A: 翻译器主要集中于预测物体的位置和内容。解码器负责优化前景物体的形状。编码器可以通过空间UNet连接来消除背景误差。

8、改进：

SwinLSTM: Improving Spatiotemporal Prediction Accuracy using Swin Transformer and LSTM

github

1、研究目标：为解决CNN方式在获取时空依赖的低效性，提出一个新的循环单元SwinLSTM。

2、难点：

3、背景：

4、方法：

5、相关研究：

6、指标：

7、分析：

8、改进：

Disentangling Physical Dynamics from Unknown Factors for Unsupervised Video Prediction

1、研究目标：利用偏微分方程的物理知识改进非监督视频预测。

2、难点：

Q1:对于视频预测任务物理定律无法在像素级上进行应用

A1: 转换到潜藏特征空间，在该空间中物理演变和残差因子可以线性解耦。

3、背景：

4、方法：

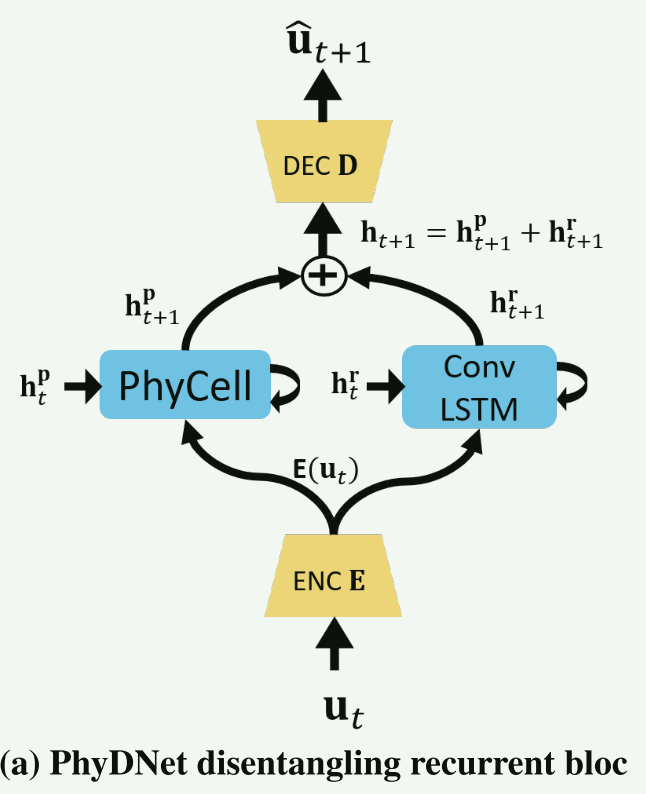
PhyDNet双分支架构：在未知变化因素上的解绑残差演化分支和在已知演变过程上的物理约束的循环分支。

视频在$t$时刻$\mathbf{p}=(x,y)$位置可以表示为$\mathbf{x}(t,\mathbf{p})$，其映射到潜藏空间$\mathfrak{H}$的特征表示为$\mathcal{H}(t,\mathbf{x})=\mathcal{H}^p(t,\mathbf{x})+\mathcal{H}^r(t,\mathbf{x})$, $\mathcal{H}^p和\mathcal{H}^r$是解耦后的物理演变成分和残差成分。视频在潜藏空间$\mathfrak{H}$的演化用偏微分方程表示为

$\frac{\partial\mathcal{H}(t,\mathbf{x})}{\partial t}=\frac{\partial\mathcal{H}^p}{\partial t}+\frac{\partial\mathcal{H}^r}{\partial t}:=\mathfrak{M}_p(\mathcal{H}^p,\mathbf{p})+\mathfrak{M}_r(\mathcal{H}^r,\mathbf{p})$​​

PhyDNet disentangling循环表达上述公式

image-20251210112612144

5、相关研究：

6、指标：

7、分析：

8、改进：

VISIONTS: Visual Masked Autoencoders Are Free-Lunch Zero-Shot Time Series Forecasters

GitHub

1、研究目标：

一个在图像上预训练的视觉模型能否成为时间序列预测的免费午餐式基础模型？

2、难点：

  • 不同样本集之间的差异，同一样本集内的异质性。

3、背景：

4、方法：

5、相关研究：

6、指标：

7、分析：

8、改进：

3D重建和渲染--------------------------------------------------------------------------------------------------------------------------

3D Gaussian Splatting for Real-Time Radiance Field Rendering

GitHub

NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

GitHub