简述

结构化数据：语音、图像、文本都是很简单的序列或者网格数据，是很结构化的数据

非结构化数据 ：网络、知识图谱、图数据结构

图结构数据是无限维的一种不规则的数据，每一个节点的周围结构可能都是独一无二的，它没有平移不变性。这种结构的数据，使得传统的CNN、RNN无法在上面工作。

非结构化数据处理难点：

图的尺度和结构复杂
节点间关系复杂
节点的特征
局部图结构不具有平移不变性

相关研究方法：GNN、DeepWalk、node2vec、GCN、GAN

同构图和异构图

在图论（Graph Theory）中，异构图（Heterogeneous Graph）和同构图（Homogeneous Graph）是两种不同的图结构概念，它们的主要区别在于节点和边的类型是否单一。

1、异构图是指节点类型和/或边类型不同的图，通常用于建模具有多种实体和关系的复杂系统。

特点：

多个节点类型（不同类别的节点）。
多个边类型（不同类别的关系）。
常用于表示复杂结构数据（如推荐系统、知识图谱等）。

2、同构图是指节点类型和/或边类型都相同的图。

图神经网络的意义

图神经网络建模目的是处理非结构化数据，通过机器学习的方法进行拟合、预测。神经网络是对单个样本的特征进行拟合，而图神经网络是在拟合单个样本特征基础之上，又加入了样本间的关系信息。

图拉普拉斯矩阵

普通拉普拉斯算子（在微积分中）：衡量的是函数在一点处的值与其周围小邻域内平均值之间的差异。它是梯度的散度，描述了函数的“平滑度”或“扩散”速率。例如，在热力学中，它描述了热量如何从高温点扩散到低温点。
图拉普拉斯算子：将上述概念从连续域（如欧几里得空间）推广到了离散域（如图结构）。它衡量的是图中一个节点的信号值与其所有邻居节点信号值平均值的差异。

所以，图拉普拉斯矩阵 L 是一个描述图结构和图上信号平滑度的数学算子。

1. 核心组件

首先需要两个矩阵：

度矩阵 (D)：一个对角矩阵。对角线上的元素 D_{ii} 是节点 i 的度（即与该节点相连的边的数量），非对角线元素为 0。
D = diag(deg(1), deg(2), ..., deg(n))
邻接矩阵 (A)：表示节点之间的连接关系。如果节点 i 和 j 之间有边，则 A_{ij} = 1，否则为 0。

2. 三种形式的拉普拉斯矩阵

组合拉普拉斯矩阵 (Combinatorial Laplacian)
- 定义： $[L]{N\times M} = [D]{N\times M} - [A]_{N\times M}$
- 解释：这是最直接的定义。(D - A)X, $[X]_{N\times M}$是节点的特征信号，这个操作正好实现了我们直观理解中的功能：“本节点的度 × 本节点的信号 - 所有邻居节点的信号之和”。想象一个描述每个节点上信号强度的向量 $\vec{f}=[X_i]_M$，那么 $L$在节点 i 上的结果就是：
  $$[L_i]M = [\deg(i) * X_i - \sum{j\in N(i)} X_j]_M$$
  这正好是节点 i 与其所有邻居 $j\in N(i)$ 的信号差异的总和。
对称归一化拉普拉斯矩阵 (Symmetric Normalized Laplacian)
- 定义： $L_{sym} = D^{-1/2} L D^{-1/2} = I - D^{-1/2} A D^{-1/2}$
- 解释：组合拉普拉斯矩阵 L 的一个问题是，高度数节点的值会很大（因为 deg(i) 大），这在高散度图中可能不稳定。归一化拉普拉斯通过节点的度对其进行了“标准化”，使得所有节点的“影响力”变得相当。它的特征值范围在 [0, 2] 之间，性质更好。
随机游走归一化拉普拉斯矩阵 (Random Walk Normalized Laplacian)
- 定义： $L_{rw} = D^{-1} L = I - D^{-1}A$
- 解释：$D^{-1}A$ 可以看作是在图上进行随机游走的转移概率矩阵。因此 $L_{rw}$ 与随机游走过程密切相关。它在分析图的随机过程性质时非常有用。

其中最常用的是组合拉普拉斯 (L) 和对称归一化拉普拉斯 (L_sym)。

图神经网络和神经网络的全连接层差异

设输入特征层X，隐藏特征层H, 权重矩阵W，邻接矩阵A(用于当前节点与相关联节点之间特征信息聚合)和激活函数$\sigma$：

神经网络：H = $\sigma$(XW)

图神经网络：H=$\sigma$(AXW)

GNN 同时接收图结构和节点特征作为输入

图神经网络和神经网络的卷积差异

神经网络：输入是像素网格，每层卷积结合来自当前像素及其相邻像素的数据计算新的当前像素数据

图神经网络：输入是图（节点和边），

图神经网络工作模式

输入图数据—>图卷机—>图全连接层—>$\left{\begin{aligned} &节点分类任务 \ &连接预测任务 \ &图与子图生成\end{aligned}\right.$

Graph Convolution Networks(GCN)

图卷积神经网络（Graph Convolutional Network）是一种能对图数据进行深度学习的方法。图卷积中的“图”是指数学（图论）中的用顶点核边建立相关联系的拓扑图。卷积指的是“离散卷积”，它的本质就是一种加权求和，加权系数就是卷积核的权重系数。

图卷积工作方式：

1、基于谱域图

将图结构数据编码成一个矩阵然后再计算矩阵的特征值。这个特征值也叫做图的谱（spectrum），被编码后的矩阵可以理解成图的谱域。使用图结构中的度和邻接矩阵来表示图的谱域。

2、基于顶点域的图

顶点域（vertex domain）也叫空间域（spatial domain）是指图的本身结构所形成的空间。使用顶点相邻间的关系以及每个顶点自己的特征属性表示顶点域。

图卷积和卷积神经网络处理数据对比

图卷积的模型所处理的数据集比深度学习模型所处理的数据集，多了一个样本间的关系维度。即，除了有每个样本自身的属性以外，还会有样本间的关联关系。

数据集

CORA数据集中有两个文件，具体说明如下。

（1）content文件包含以下格式的论文说明：

每行的第一个条目包含论文的唯一字符串ID，后跟二进制值，指示词汇表中的每个单词在纸张中是否存在（由1表示）或不存在（由0表示）。最后，行中的最后一项包含纸张的类标签。

（2）cites文件包含了语料库的引文图。每一行用以下格式描述一个链接：

每行包含两个纸张ID。第一个条目是被引用论文的ID，第二个ID代表包含引用的论文。链接的方向是从右向左的。如果一行用“paper1 paper2”表示，则链接为“paper2->paper1”。

DGL库中的数据集

Sst：（ Stanford sentiment treebank dataset 斯坦福情感树库数据集）每个样本都是一个树结构的句子。叶节点代表单词。每个节点还具有情感注释：5类（非常消极，消极，中立，积极和非常积极）。
KarateClub：（ Karate Club dataset 空手道俱乐部数据集）数据集中只有一个图，图中的节点描述了社交网络中的用户是否是空手道俱乐部中的成员。
CitationGraphDataset：（ Citation Graph dataset 引文网络数据集）节点表示作者，边缘表示引用关系。
CoraDataset：（ Cora Citation Network dataset Cora引用网络数据集）节点表示作者，边表示引用关系。详见9.4.1小节。
CoraFull：（ CoraFull dataset CoraFull数据集）Cora的扩展，节点表示论文，边表示论文间引用关系。
AmazonCoBuy：（ Amazon Co-Purchase dataset 亚马逊共同购买数据集）节点代表商品，边缘表示经常一起购买两种商品。节点特征是产品的评论，节点的类别标签是产品的类别。
Coauthor：（ Coauthor dataset 合著者数据集）节点是作者，边是共同撰写过论文的关系。节点特征是作者论文中的论文关键词，节点类别标签是作者的研究领域。
BitcoinOTC：（ BitcoinOTC dataset 比特币OTC平台数据集）用户在比特币OTC平台进行交易的信任网络。每个节点代表一个用户，用-10（完全不信任）至+10（完全信任）的等级对其进行评分。
QM7b：（ QM7b dataset QM7b数据集）该数据集由7,211个分子组成，所有的分子可以回归到14个分类目标。节点表示原子，边缘表示键。
MiniGCDataset：（ Mini graph classification dataset 迷你图分类数据集）数据集包含8种不同类型的图形。（包括循环图、星形图、车轮图、棒棒糖图、超立方体图、网格图、集团图、圆形梯形图）
TUDataset：（ Graph kernel dataset 图内核数据集）图形分类的图形内核数据集。
GINDataset：（ Graph isomorphism network dataset 图同构网络数据集）图内核数据集的紧凑子集，数据集包含流行的图形内核数据集的紧凑格式，其中包括：4个生物信息学数据集（MUTAG，NCI1，PROTEINS，PTC）和5个社交网络数据集（COLLAB，IMDBBINARY，IMDBMULTI， REDDITBINARY，REDDITMULTI5K）。
PPIDataset：（ Protein-Protein Interaction dataset 蛋白质-蛋白质相互作用数据集）数据集包含24个图。每个图的平均节点数为2372。每个节点具有50个要素和121个标签。

数学描述

$\mathcal{G}=(\mathcal{V,E}), u\in\mathcal{V}, v\in\mathcal{V}, (u,v)\in\mathcal{E}$
简单图：节点间至多只有一条边，自己和自己没有边，边是无向的。 $(u, v)\in\mathcal{E}\leftrightarrow (v, u)\in\mathcal{E}$
图也可以用邻接矩阵表达，邻接矩阵$A\in\mathbb{R}^{|\mathcal{V}|\times|\mathcal{V}|}$, 无向图A是对称矩阵，有向图是非对称矩阵。
边除了有向、无向、权重的差异，边还可以有不同的类型，设边的类型为$\tau$, $(u,\tau,v)\in\mathcal{E}$, 不同类型的邻接矩阵可表示为$A_\tau$, 该图可称为多关系图$A\in\mathbb{R}^{|\mathcal{V}|\times|\mathcal{R}|\times|\mathcal{V}|}$, 多关系图可分为异构图和多重图。
- 异构图：除了边可以有多种类型，节点也可有多种类型，同时边的类型取决于节点的类型。
  
  $$\mathcal{V}=\mathcal{V}_1\cup\mathcal{V}_2\cup\cdots\cup\mathcal{V}_k, \mathcal{V}_i\cap\mathcal{V}_j=\emptyset，\forall i\neq j$$
  
  $$(u,\tau_i,v)\in\mathcal{E}\rightarrow u\in\mathcal{V}_j, u\in\mathcal{V}_k$$
- 多重图：特殊异构图，不同类型的边只能连接不同类型的节点，相同类型的边只能连接相同类型的节点。图可分解成多层，每一类型的节点占据一层，层内的节点关系是相同类型，不同层间的节点关系类型不同。

$$(u,\tau_i,v)\in\mathcal{E}\rightarrow u\in\mathcal{V}_j, u\in\mathcal{V}_k \and j \neq k $$

任务分类

监督任务：在给定输入数据时，预测输出。
非监督任务：在数据中推理出数据间的不同模式。
节点分类：预测节点$u$的标签$y_u$, 该标签可以是节点类型、节点属性或节点类别。

图中的节点是存在连接的，因此节点应该是非独立和非同分布的。

关系预测：预测图中节点之间的边。连接预测、图补完、关系推理。给定一组节点和一部分的边，利用上述信息推断缺失的边。
节点聚类检测：检测图中哪些节点更有可能与其他节点生成边。
图的分类、回归和聚类：数据不再是图中的节点、边等元素，而是不同的图，目标是对图做预测和分类以及聚类出相似的图。

传统研究图的方法

基础的图统计
核方法
测量节点邻域重叠
谱聚类

图统计

节点级特征

节点的度：节点上边的数目。$d_u=\sum_{v\in\mathcal{V}}A[u,v], u\in\mathcal{V}$，描绘一个节点的邻域数目。
节点中心度(矢量)：描绘在图中随机游走无限长的距离后一个节点被访问到的几率。利用节点间的递推关系定义，一个节点的中心度正比于邻接节点的中心度的平均值。$e_u = \frac{1}{\lambda}\sum_{v\in\mathcal{V}}A[u,v]e_v, \forall u\in\mathcal{V}$
聚集系数：在节点邻域中封闭的三角形所占比例。$$c_u = \frac{|(v_1,v2)\in\mathcal{E}: v_1,v_2\in\mathcal{N}(u)|}{\left(\begin{align*}d_u \ 2\end{align*}\right)}$$, $\left(\begin{align*}d_u \ 2\end{align*}\right)$表示u邻域中所有可能成对的节点数量。
封闭三角
节点自身中心图

图级特征

打包节点特征：定义图的特征只需要汇聚各节点特征。该图特征完全依赖于局部节点特征，遗漏全局特征。
核计算：提取局部节点特征，使用核函数汇聚特征，作为图特征。
1. 初始化每一个节点标签$l^{(0)}(v)=d_v \forall v\in\mathcal{V}$
2. 利用hash将前一次邻域节点标签特征向量映射成当前节点标签特征标量。$l^{(i)} = HASH(\textbraceleft\textbraceleft l^{(i-1)}(u) \forall u\in\mathcal{N(v)}\textbraceright\textbraceright)$
3. 迭代 K次得到K跳邻域结构特征，计算该特征的统计分布表示图特征。
子图和基于路径方法：

统计不同子图结构的出现次数。路径方法用不同路径替换不同子图，即随机游走若干步统计不同特征值（节点的度）出现的次数（分布）

关系预测

邻域重叠检测：描述连个节点之间相关的程度。
- 两个节点邻域之间共有节点的数量。$S[u,v]=|\mathcal{N}(u)\cap \mathcal{N}(v)|$，表示相似矩阵。假设邻接矩阵存在边的几率正比于相似矩阵，$P(A[u,v]=1)\propto S[u,v]$
- Sorensen矩阵$S_{Sorenson}[u,v]=\frac{2|\mathcal{N}(u)\cap \mathcal{N}(v)|}{d_u+d_v}$, 用节点的度做归一化，不做归一化预测偏向度大的节点
- Salton矩阵$S_{Salton}[u,v]=\frac{2|\mathcal{N}(u)\cap \mathcal{N}(v)|}{\sqrt{d_ud_v}}$
- Jaccard矩阵$S_{Jaccard}[u,v]=\frac{|\mathcal{N}(u)\cap \mathcal{N}(v)|}{|\mathcal{N}(u)\cup \mathcal{N}(v)|}$
- Resource Allocation矩阵$S_{RA}[v_1,v_2]=\sum_{u\in\mathcal{N}(v_1)\cap \mathcal{N}(v_2)}\frac{1}{d_u}$
- Adamic-Adar矩阵$S_{AA}[v_1,v_2]=\sum_{u\in\mathcal{N}(v_1)\cap \mathcal{N}(v_2)}\frac{1}{\log(d_u)}$
全局重叠测量：两个节点在其邻域上没有重叠但是根据更大的区域判断依旧可能是连接的。
- Katz矩阵：计算两个节点之间所有路径的数量。并且可以设置不同路径长度对生成关系的影响权重，受节点度的影响。$S_{Katz}[u,v]=\sum_{i=1}^{\infty}\beta^iA^i[u,v]$
- $\frac{A^i}{\mathbb{E}[A^i]}$: 两节点之间实际路径数量比两节点间路径数量的期望。
- 路径长度为1的节点相连$\mathbb{E}[A[u,v]]=\frac{d_ud_v}{2|\mathcal{E}|}$: 随机配置一个具有相同度的图，在此图中，两节之间存在边的概率正比于两节点度数的乘积。有$d_u$条边离开u节点，其中每一个边有$\frac{d_v}{2|\mathcal{E}|}$大几率连接到节点v。
  
  路径长度为2的节点相连，…，
  
  用最大邻接矩阵的特征值近似路径长度增加后路径数量的变化量。$\mathbb{E}[A^i[u,v]]=\frac{d_ud_v\lambda_1^{i-1}}{2|\mathcal{E}|}$
- LNH矩阵(归一化的Katz矩阵)：$S_{LNH}[u,v]=I[u,v]+\frac{2m}{d_ud_v}\sum_{i=0}^{\infty}\beta^i\lambda_1^{1-i}A^i[u,v]$
- 除了使用统计路径数量也可以考虑使用随机游走方法。$S_{RW}[u,v]=\bold{q}_u[v]+\bold{q}_v[u]$存在边几率正比于通过随机游走从另一个节点到达该节点的几率。

图中节点聚集

图拉普拉斯和谱方法
- 非归一化拉普拉斯矩阵$L=D-A$, A是邻接矩阵，D是度矩阵。数学性质：
  1. 拉普拉斯矩阵具有对称性$L=L^T$，半正定性$\bold{x}^TL\bold{x}\ge0, \forall \bold{x}\in \mathbb{R}^{|\mathcal{V}|}$。
  2. $\begin{align*}\bold{x}^TL\bold{x}&=\frac{1}{2}\sum_{u\in\mathcal{V}}\sum_{v\in\mathcal{V}}Au,v^2 \ &= \sum_{(u,v)\in\mathcal{E}}(\bold{x}[u]-\bold{x}[v])^2\end{align*}$
  3. 拉普拉斯矩阵有$|\mathcal{V}|$多个非负特征值，0特征值的重复数对应边的数目。
- 归一化拉普拉斯矩阵
  - 对称归一化$L_{sym}=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$
  - 随机游走归一化$L_{RW}=D^{-1}L$
聚集
- 属于同一个0特征值的特征向量可以使聚集在一起因为他们彼此相连。
- 图切割：
  
  图中节点$\mathcal{V}$的子集$\mathcal{A}\subset\mathcal{V}$和其补集$\bar{\mathcal{A}}$, 对图中节点分割为K个区域并且彼此之间无交集$\mathcal{A}_1,…,\mathcal{A}_K$, 图的分割值定义为跨各区域边界的边的数目：
  
  $$cut(\mathcal{A}_1,…,\mathcal{A}K)=\frac{1}{2}\sum{k=1}^{K}|(u,v)\in\mathcal{E}: u\in\mathcal{A}_k, v\in\bar{\mathcal{A}}_k|$$
- 简单的优化聚集：节点聚集成K个区域的的最优方案是选择一种划使分割值最小。容易出现聚集的区域只有一个节点。
- 最小化比例切割值：最小化分割数的同时最大化各分割区域。
  
  $$RatioCut(\mathcal{A}_1,…,\mathcal{A}K)=\frac{1}{2}\sum{k=1}^{K}\frac{|(u,v)\in\mathcal{E}: u\in\mathcal{A}_k, v\in\bar{\mathcal{A}}_k|}{|\mathcal{A}_k|}$$
- 最小化归一化切割：让聚集的节点有近似数目的入射边。
  
  $$NCut(\mathcal{A}_1,…,\mathcal{A}K)=\frac{1}{2}\sum{k=1}^{K}\frac{|(u,v)\in\mathcal{E}: u\in\mathcal{A}_k, v\in\bar{\mathcal{A}}k|}{\sum{u\in\mathcal{A}_k}d_u}$$

传统统计特征需要人工统计构建特征，不灵活、费时、构建过程繁琐。

节点嵌入和邻域重构

节点嵌入是对节点进行编码得到一个向量表示，记录了节点在图中的位置信息和节点邻域结构信息。

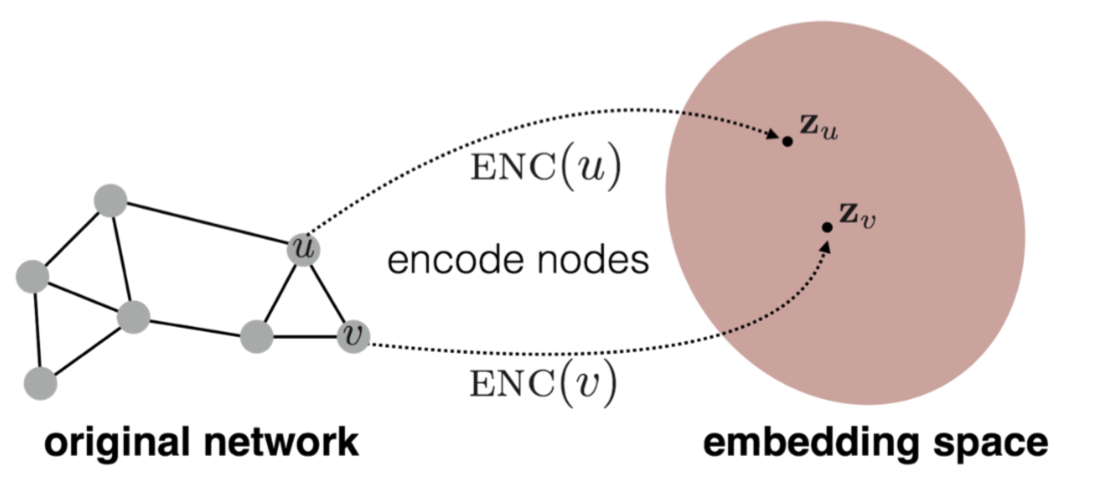
编解码架构

编码器将图中节点映射为低维度向量或嵌入量。解码器提取嵌入量并使用他们重构节点邻域信息。

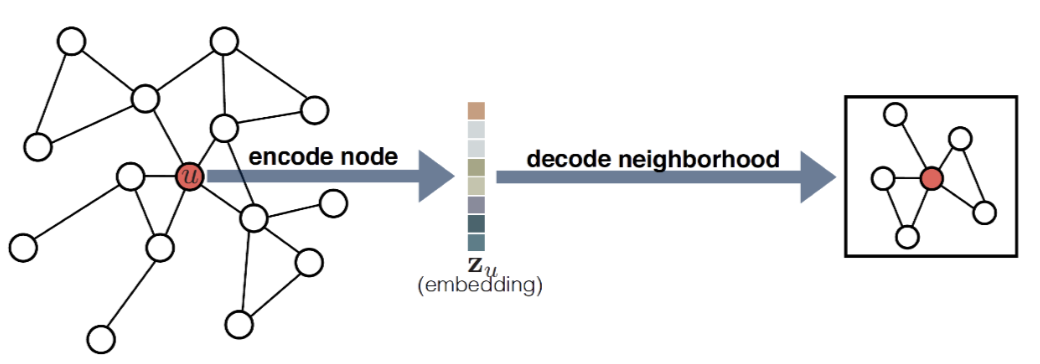
编码

节点$v\in\mathcal{V}$，嵌入量$\bold{z}_v\in\mathbb{R}^d$, 向量维度d，$encoder: \mathcal{V}\rightarrow\mathbb{R}^d$. 编码器将节点id作为输入，将嵌入向量作为输出。编码器可以看作是一个基于节点id的嵌入查询函数(浅嵌入方法)$encoder(v)=Z[v]$, $Z\in\mathbb{R}^{|\mathcal{V}|\times d}$。除了节点id作为输入也可以使用节点特征或者局部图结构（图神经网络）。

解码

解码器使用节点嵌入向量$\bold{z}_u$作为输入，输出或预测该节点的邻域集合$\mathcal{N}(u)$或者该节点对应的邻接矩阵的行$A[u]$。一般使用成对的解码器预测(重构)两节点是否存在关系（边）或者两个节点是否是相似的$decoders:\mathbb{R}^d\times\mathbb{R}^d\rightarrow\mathbb{R}^+$，$decoders(encoder(u), encoder(v))=decoders(\bold{z}_u,\bold{z}_v)$。优化目标就是最小化编解码后的重构损失，重构损失是图的重构矩阵与图的相似矩阵之差。图相似矩阵通过统计图的邻域重叠获取。

优化目标

训练集：一组节点对集合$\mathcal{D}$, 而不是边集合$\mathcal{E}$。
节点对的重构损失$\mathcal{l}(decoders(\bold{z}_u,\bold{z}_v), S[u,v])$：节点对重构的相似值$decoders(\bold{z}_u,\bold{z}_v)$与实际相似值$S[u,v]$的差异。可以用方均误差，分类损失，交叉熵。
节点对集合上的累积损失：$\mathcal{L} = \sum_{(u,v)\in\mathcal{D}}\mathcal{l}(decoders(\bold{z}_u,\bold{z}_v), S[u,v])$