蚁群算法

蚁群算法（Ant Colony Optimization, ACO） 是一种基于群体智能的元启发式算法，灵感来源于蚂蚁觅食行为。蚂蚁在寻找食物时，会通过释放信息素（pheromone）来标记路径，其他蚂蚁会根据信息素的浓度选择路径。通过模拟这一行为，ACO 可以有效地解决组合优化问题，如旅行商问题（TSP）。

蚁群算法的基本思想

  1. 蚂蚁的路径选择：

    • 每只蚂蚁根据信息素浓度和启发式信息（如距离）选择下一个要访问的城市。
    • 信息素浓度越高，路径被选择的概率越大。

  2. 信息素更新：

    • 蚂蚁完成一次遍历后，会根据路径的长度更新信息素。
    • 路径越短，信息素增加得越多。

  3. 正反馈机制：

    • 信息素的积累和挥发形成正反馈机制，使得较优路径的信息素浓度逐渐增加。

TSP问题描述

假设有n个城市，城市之间的距离用一个距离矩阵$D$表示， $D_{ij}$表示城市i,j之间的距离。目标是找到一个路径或排列$\pi=(\pi_1,\pi_2, …, \pi_n)$,使得以下总距离最小：

蚁群算法解决 TSP 的步骤

  1. 初始化：

    • 初始化信息素矩阵$\tau$，通常设置为一个较小的常数。
    • 初始化启发式信息矩阵 $ \eta $，通常为距离的倒数 $ \eta{ij} = \frac{1}{D{ij}} $。

  2. 蚂蚁的路径构建：

    • 每只蚂蚁从起点出发，根据概率选择下一个城市，直到访问完所有城市。
    • 单只蚂蚁选择概率公式：其中：
      • $ \tau_{ij} $ 是信息素浓度。
      • $ \eta_{ij} $ 是启发式信息。
      • $ \alpha $ 和 $ \beta $ 是控制信息素和启发式信息权重的参数。

  3. 信息素更新：

    • 所有蚂蚁（蚂蚁有m只）完成各自路径构建后，更新信息素：其中：
      • $ \rho $ 是信息素挥发率。
      • $ \Delta \tau_{ij}^k $ 是第 $ k $ 只蚂蚁在路径 $ (i, j) $ 上释放的信息素，通常与路径长度成反比：
        • $ Q $ 是常数。
        • $ L_k $ 是蚂蚁 $ k $ 的走过的路径长度。

  4. 迭代：

    • 重复路径构建和信息素更新过程，直到达到最大迭代次数或找到满意解。

代码实现（Python）

以下是使用蚁群算法解决 TSP 的 Python 实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
import numpy as np

class AntColony:
    def __init__(self, distances, n_ants, n_iterations, decay, alpha=1, beta=2):
        """
        初始化参数：
        - distances: 距离矩阵
        - n_ants: 蚂蚁数量
        - n_iterations: 迭代次数
        - decay: 信息素挥发率
        - alpha: 信息素权重
        - beta: 启发式信息权重
        """
        self.distances = distances
        self.n_ants = n_ants
        self.n_iterations = n_iterations
        self.decay = decay
        self.alpha = alpha
        self.beta = beta
        self.n_cities = len(distances)
        self.pheromone = np.ones((self.n_cities, self.n_cities))  # 初始化信息素矩阵

    def run(self):
        best_path = None
        best_distance = float('inf')

        for iteration in range(self.n_iterations):
            all_paths = self._build_paths()
            self._update_pheromone(all_paths)

            # 更新最优路径
            shortest_path = min(all_paths, key=lambda x: x[1])
            if shortest_path[1] < best_distance:
                best_distance = shortest_path[1]
                best_path = shortest_path[0]

            print(f"Iteration {iteration + 1}: Best Distance = {best_distance}")

        return best_path, best_distance

    def _build_paths(self):
        all_paths = []
        for _ in range(self.n_ants):
            path = self._build_single_path()
            distance = self._calculate_distance(path)
            all_paths.append((path, distance))
        return all_paths

    def _build_single_path(self):
        path = []
        visited = set()
        start_city = np.random.randint(self.n_cities)  # 随机选择起点
        path.append(start_city)
        visited.add(start_city)

        while len(visited) < self.n_cities:
            next_city = self._choose_next_city(path[-1], visited)
            path.append(next_city)
            visited.add(next_city)

        return path

    def _choose_next_city(self, current_city, visited):
        probabilities = []
        for city in range(self.n_cities):
            if city not in visited:
                pheromone = self.pheromone[current_city][city]
                distance = self.distances[current_city][city]
                probabilities.append((pheromone ** self.alpha) * ((1 / distance) ** self.beta))
            else:
                probabilities.append(0)

        probabilities = np.array(probabilities)
        probabilities /= probabilities.sum()  # 归一化
        next_city = np.random.choice(range(self.n_cities), p=probabilities)
        return next_city

    def _calculate_distance(self, path):
        distance = 0
        for i in range(len(path) - 1):
            distance += self.distances[path[i]][path[i + 1]]
        distance += self.distances[path[-1]][path[0]]  # 回到起点
        return distance

    def _update_pheromone(self, all_paths):
        self.pheromone *= (1 - self.decay)  # 信息素挥发
        for path, distance in all_paths:
            for i in range(len(path) - 1):
                self.pheromone[path[i]][path[i + 1]] += 1 / distance
            self.pheromone[path[-1]][path[0]] += 1 / distance  # 回到起点

# 示例
distances = np.array([
    [0, 10, 15, 20],
    [10, 0, 35, 25],
    [15, 35, 0, 30],
    [20, 25, 30, 0]
])

ant_colony = AntColony(distances, n_ants=10, n_iterations=100, decay=0.1, alpha=1, beta=2)
best_path, best_distance = ant_colony.run()
print("Best Path:", best_path)
print("Best Distance:", best_distance)

参数说明

  • 蚂蚁数量（n_ants）：蚂蚁数量越多，搜索能力越强，但计算成本也越高。
  • 迭代次数（n_iterations）：迭代次数越多，算法越有可能找到更优解。
  • 信息素挥发率（decay）：控制信息素的挥发速度，通常取值在 0.1 到 0.5 之间。
  • 信息素权重（alpha）：控制信息素对路径选择的影响。
  • 启发式信息权重（beta）：控制启发式信息（如距离）对路径选择的影响。

总结

  • 蚁群算法是一种基于群体智能的优化算法，适合解决 TSP 等组合优化问题。
  • 通过模拟蚂蚁觅食行为，算法能够逐步找到较优解。
  • 算法的性能受参数设置影响较大，需要根据具体问题进行调整。
  • 蚁群算法的优势在于其并行性和鲁棒性，适合解决大规模复杂问题。

退火算法

模拟退火算法（Simulated Annealing, SA） 是一种基于概率的全局优化算法，灵感来源于固体退火过程。它通过引入“温度”参数和概率接受机制，能够在搜索过程中跳出局部最优解，逐步逼近全局最优解。模拟退火算法非常适合解决组合优化问题，如旅行商问题（TSP）。

模拟退火算法的基本思想

  1. 初始解：从一个初始解（例如随机路径）开始。
  2. 邻域搜索：在当前解的邻域中生成一个新解。
  3. 接受准则：
    • 如果新解比当前解更优，则接受新解。
    • 如果新解比当前解差，则以一定概率接受新解。概率由以下公式决定：其中：
      • $\Delta E$ 是新解与当前解的目标函数值差。
      • $T$ 是当前温度。
  4. 降温：随着迭代次数增加，逐步降低温度 $T$。
  5. 终止条件：当温度降到某个阈值或达到最大迭代次数时，算法结束。

模拟退火算法解决 TSP 的步骤

以下是使用模拟退火算法解决 TSP 的具体步骤：

1. 初始化

  • 生成一个初始路径（例如随机排列）。
  • 设置初始温度 $T_0$ 和降温速率 $\alpha$。
  • 设置终止温度 $T_{\text{min}}$ 和最大迭代次数。

2. 邻域搜索

在当前路径的邻域中生成一个新路径。常用的邻域操作包括：

  • 交换：随机选择两个城市并交换它们的位置。
  • 逆序：随机选择一段路径并逆序排列。
  • 插入：随机选择一个城市并插入到另一个位置。

3. 接受准则

计算新路径的总距离 $E{\text{new}}$ 和当前路径的总距离 $E{\text{current}}$：

  • 如果 $E{\text{new}} < E{\text{current}}$，接受新路径。
  • 如果 $E{\text{new}} \geq E{\text{current}}$，以概率 $P = \exp\left(-\frac{E{\text{new}} - E{\text{current}}}{T}\right)$ 接受新路径。

4. 降温

更新温度：

其中 $\alpha$ 是降温速率（通常取 $0.8 \leq \alpha \leq 0.99$）。

5. 终止条件

当温度降到 $T_{\text{min}}$ 或达到最大迭代次数时，算法结束。

代码实现（Python）

以下是使用模拟退火算法解决 TSP 的 Python 实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
import math
import random

# 计算路径总距离
def calculate_distance(path, distances):
    distance = 0
    for i in range(len(path) - 1):
        distance += distances[path[i]][path[i + 1]]
    distance += distances[path[-1]][path[0]]  # 回到起点
    return distance

# 生成初始路径
def generate_initial_path(n_cities):
    path = list(range(n_cities))
    random.shuffle(path)
    return path

# 邻域操作：交换两个城市
def swap_cities(path):
    new_path = path.copy()
    i, j = random.sample(range(len(path)), 2)
    new_path[i], new_path[j] = new_path[j], new_path[i]
    return new_path

# 模拟退火算法
def simulated_annealing(distances, T0=1000, alpha=0.99, T_min=1e-3, max_iter=1000):
    n_cities = len(distances)
    current_path = generate_initial_path(n_cities)
    current_distance = calculate_distance(current_path, distances)
    best_path = current_path.copy()
    best_distance = current_distance

    T = T0
    for iteration in range(max_iter):
        if T < T_min:
            break

        # 生成新路径
        new_path = swap_cities(current_path)
        new_distance = calculate_distance(new_path, distances)

        # 计算能量差
        delta_E = new_distance - current_distance

        # 接受准则
        if delta_E < 0 or random.random() < math.exp(-delta_E / T):
            current_path = new_path
            current_distance = new_distance

            # 更新最优解
            if current_distance < best_distance:
                best_path = current_path.copy()
                best_distance = current_distance

        # 降温
        T *= alpha

        # 打印当前状态
        if iteration % 100 == 0:
            print(f"Iteration {iteration}: Best Distance = {best_distance}, Temperature = {T}")

    return best_path, best_distance

# 示例
distances = [
    [0, 10, 15, 20],
    [10, 0, 35, 25],
    [15, 35, 0, 30],
    [20, 25, 30, 0]
]

best_path, best_distance = simulated_annealing(distances)
print("Best Path:", best_path)
print("Best Distance:", best_distance)

参数说明

  • 初始温度 $T_0$：控制初始接受劣解的概率，通常设置为一个较大的值（如 1000）。
  • 降温速率 $\alpha$：控制温度的下降速度，通常取 $0.8 \leq \alpha \leq 0.99$。
  • 终止温度 $T_{\text{min}}$：当温度降到该值时，算法停止。
  • 最大迭代次数：算法的最大运行次数。

总结

  • 模拟退火算法是一种全局优化算法，适合解决 TSP 等组合优化问题。
  • 通过引入温度和概率接受机制，算法能够跳出局部最优解，逐步逼近全局最优解。
  • 算法的性能受参数设置影响较大，需要根据具体问题进行调整。
  • 模拟退火算法的优势在于其简单性和鲁棒性，适合解决中小规模问题。

订单拣选问题

问题概述：
订单拣选问题由一组需要准备交付给不同客户的订单组成。每个订单都由一组订单项目（请求的产品）组成。这些产品位于仓库或超市的货架上，并占用特定体积的空间。为了完成订单，超市中有一组可用的手推车，它们遵循计算的路径并拣选订单项目。在此路径的每个步骤中选取一个订单项。产品在仓库中的位置决定了手推车的路径，每个手推车中的空间被划分为多个具有指定容量的桶。订单拣选问题的目标是计算一个拣选计划，该计划为每个手推车提供路径并考虑以下约束：

  • 手推车的行驶距离被最小化。

  • 必须拣选所有订单项。

  • 来自不同订单的商品不得混合在同一个桶中，因此必须为将在同一手推车上准备的每个订单预留足够的桶。

  • 应尽量减少将订单拆分为不同的手推车。

    image-20250210155157128

为了表述问题，仓库被定义为一组组织成列和行的货架。商品位于特定货架的左侧或右侧的特定行上。货架、侧边和行决定了产品位置。

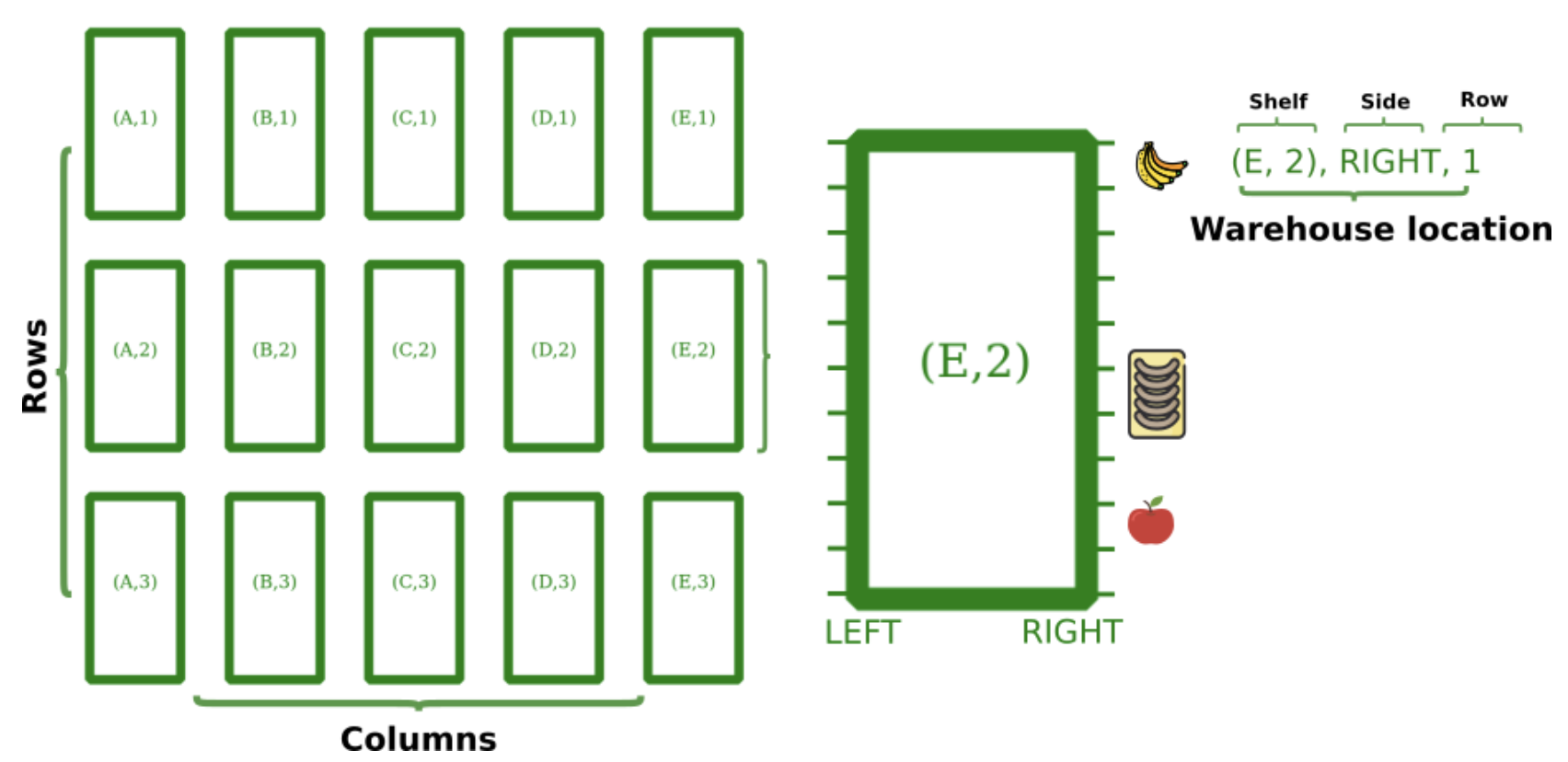
image-20250210163159226

博客https://www.optaplanner.org/blog/2021/10/14/OrderPickingQuickstart.html

类比到智能巡检排程项目：

  • 订单：检修任务
  • 订单项：检修部件，检修的部件占用一定的发电损失，检修部件位于风场的风机上。
  • 手推车：检修人员。
  • 手推车行驶距离最小：发电量损失最小。
  • 不同部件不得同一时间让同一个检修员检修。
  • 同一风机的所有部件检修完前不得检修另一个风机的部件。